Nêu số đo góc (theo mẫu).
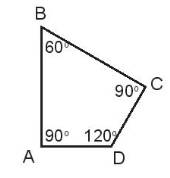
| Góc | Số đo góc |
| Góc đỉnh A; cạnh AB, AD | 90o |
| Góc đỉnh B; cạnh BA, BC | ? |
| Góc đỉnh C; cạnh CB, CD | ? |
| Góc đỉnh D; cạnh DA, DC | ? |
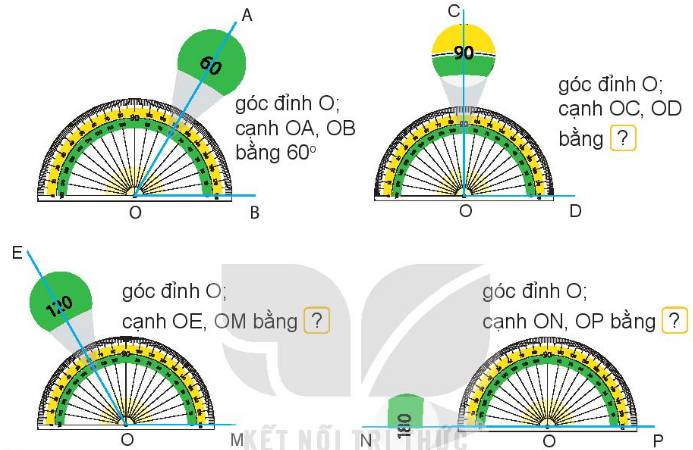
Quan sát thước đo góc rồi nêu số đo của mỗi góc (theo mẫu).
Nêu cách tính số đo của góc có đỉnh ở bên trong đường tròn theo số đo của các cung bị chắn.
Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo các cung bị chắn.
Nêu cách tính số đo của góc có đỉnh ở bên ngoài đường tròn theo số đo của các cung bị chắn.
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo của các cung bị chắn.
Nêu cách tính số đo của góc có đỉnh ở bên ngoài đường tròn theo số đo của các cung bị chắn.
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo của các cung bị chắn.
Nêu cách tính số đo của góc có đỉnh ở bên trong đường tròn theo số đo của các cung bị chắn.
Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo các cung bị chắn.
a,Tính góc ở đỉnh của một ∆ cân biết góc ở đáy của ∆ đó =50°
b,__________đáy___________________________đỉnh___________70°
c,Biết∆ABC cân tại A ,hãy tính số đo góc B và C theo số đo góc A
a, vì tam giác có góc ở đáy bằng 50 độ nên góc còn lại cũng bằng 50 độ. ta coi góc ở đỉnh là A thì A+50+50=180(độ) nên A=80 độ
b,gọi 2 góc ở đáy là B thì 70+B+B=180 nên B=55 độ
c, gọi số đo góc A lã, 2 góc còn lại là y thì x+y+y=180 nên y=180/2x=90/x
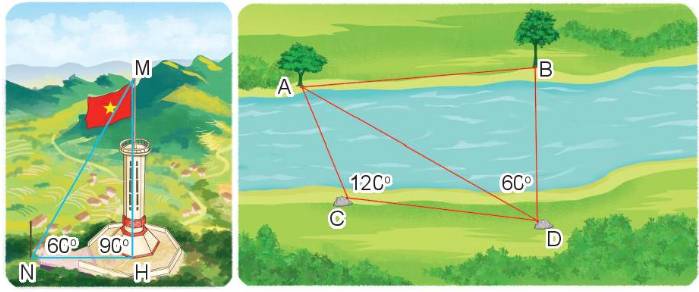
Quan sát tranh rồi nêu số đo các góc sau:
góc đỉnh N; cạnh NM, NH bằng  , góc đỉnh H; cạnh HM, HN bằng
, góc đỉnh H; cạnh HM, HN bằng 
góc đỉnh C; cạnh CA, CB bằng  , góc đỉnh D; cạnh DA, DB bằng
, góc đỉnh D; cạnh DA, DB bằng 
góc đỉnh N; cạnh NM, NH bằng 600, góc đỉnh H; cạnh HM, HN bằng 900
góc đỉnh C; cạnh CA, CB bằng 350, góc đỉnh D; cạnh DA, DB bằng 450
cho đường thẳng M và song saong với nhau đường thẳng t cắt đường thẳng m,n theo thứ tự A và b . biết 1 gó đỉnh b=110 độ
a, tính số đo các góc ở đỉnh A
b, tính tổng số đo 1 cặp góc cùng phía
Cho góc xOy có số đo 70°.
a) Vẽ góc x’Oy’ đối đỉnh với góc xOy. Tính số đo góc x’Oy’.
b) Hai góc x’Oy và xOy’ có đối đỉnh với nhau không, vì sao?
c)Tính số đo các góc x’Oy và xOy’.
\(a,\widehat{x'Oy'}=\widehat{xOy}=70^0\left(2.góc.đđ\right)\)
\(b,\widehat{x'Oy}.đối.đỉnh.\widehat{xOy'}\) do \(Ox.đối.Ox';Oy.đối.Oy'\)
\(c,\widehat{xOy'}+\widehat{xOy}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xOy'}=180^0-70^0=110^0\\ \widehat{xOy'}=\widehat{x'Oy}=110^0\left(đối.đỉnh\right)\)