Vẽ tam giác MPN biết MN=2,5cm,NP=3cm,PM=5cm

Những câu hỏi liên quan
Vẽ tam giác MNP biết MN = 2,5cm, NP = 3cm, PM = 5cm.
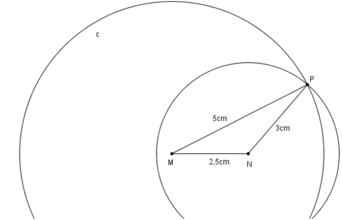
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
Đúng 0
Bình luận (0)
Vẽ tam giác MNP biết MN = 2,5cm, NP = 3cm, PM = 4cm ?
-Vẽ đoạn MN= 2,5cm
- Trên cùng một nửa mặt phẳng bở MN vẽ cung trong tâm M bán kính 5cm và cung tròn tâm N bán kinh 5cm.
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn MN, NP, ta được tam giác MNP.
Đúng 0
Bình luận (1)
vẽ tam giác mnp biết MN=2,5 cm,NP=3cm, PM=5cm
Xem thêm câu trả lời
vẽ vào vở tam giác MNP biết MN=2,5 cm ;NP=3 cm;PM=5cm
b)vẽ vào vở tam giác EFG có EF=FG=GE=3cm sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc
Cho ΔABC có AB 4cm, BC 6cm, AC 5cm. ΔMNP có MN 3cm, NP 2,5cm, PM 2cm thì tỉ lệ
S
M
N
P
S
A
B
C
bằng bao nhiều? A.
1
3
B.
1
4
C.
1
8
D....
Đọc tiếp
Cho ΔABC có AB = 4cm, BC = 6cm, AC = 5cm. ΔMNP có MN = 3cm, NP = 2,5cm, PM = 2cm thì tỉ lệ S M N P S A B C bằng bao nhiều?
A. 1 3
B. 1 4
C. 1 8
D. 1
Ta có:
M N B C = 3 6 = 1 2 , P N C A = 2 , 5 5 = 1 2 , P M A B = 2 4 = 1 2 ⇒ M N B C = P N C A = P M A B = 1 2
Vậy ΔPMN ~ ΔABC (c - c - c)
Suy ra tỉ số đồng dạng k của hai tam giác là k = M N B C = 1 2
⇒ S M N P S A B C = k 2 = ( 1 2 ) 2 = 1 4
Đáp án: B
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB 4cm, BC 5cm, AC 6cm; tam giác MNP có MN 2cm, NP 3CM, MP 2,5cm. Cách viết nào sau đây đúng quy ước về đỉnh A.
Δ
A
B
C
∽
Δ
M
N
P
;
B.
Δ
A
B
C
∽
Δ
M
P
N
;
C.
Δ
A
B
C
∽
Δ
N...
Đọc tiếp
Cho tam giác ABC có AB = 4cm, BC =5cm, AC = 6cm; tam giác MNP có MN = 2cm, NP = 3CM, MP= 2,5cm. Cách viết nào sau đây đúng quy ước về đỉnh
A. Δ A B C ∽ Δ M N P ;
B. Δ A B C ∽ Δ M P N ;
C. Δ A B C ∽ Δ N P M ;
D. Δ A B C ∽ Δ N M P .
bài 1: vẽ đoạn thẳng AB =6cm vẽ đường tròn tâm A bán kính 3cm ,vẽ đường tròn tâm B bán kính 4 cm.Đường tròn (A;3cm) cắt (B;4cm) tại C và D .Tính chu vi tam giác ACB và tam giác ADB ?
bài 2 Nêu cách vẽ tam giác MNP biết MN=5cm,NP=3m,PM=7cm
<help meeeeeee>thanks
Cho tam giác ABC có độ dài các cạnh
A
B
4
c
m
,
A
C
5
c
m
v
à
B
C
6
c
m
và tam giác MNP có độ dài các cạnh
M
N
3
c
m
,
M
P
2
c
m
,
N
P
...
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh A B = 4 c m , A C = 5 c m v à B C = 6 c m và tam giác MNP có độ dài các cạnh M N = 3 c m , M P = 2 c m , N P = 2 , 5 c m thì:
A. S A B C S M N P = 4
B. S M N P S A B C = 1 2
C. S M N P S A B C = 1 3
Cho tam giác ABC có AB=3cm,BC=5cm,AC=6cm và tam giác MNP có MN=9cm,NP=4,5cm,PM=7,5cm.
CMR: tam giác ABC∼tam giác NPM
Giups mk vs ạ ai nhanh mk tick nha :>
Xét ΔABC và ΔNPM có
\(\dfrac{AB}{NP}=\dfrac{AC}{NM}=\dfrac{BC}{PM}\)
Do đó: ΔABC∼ΔNPM
Đúng 2
Bình luận (0)




















