
Những câu hỏi liên quan
Một học sinh dùng thì kế để đo thời gian rơi tự do của một vật. Ba lần đo cho kết quả là 0,404 s; 0,406 s; 0,403 s. Sai số của đồng hồ đo là 0,001s. kết quả của phép đo thời gian rơi tụ do của vật được ghi là ?
Xem chi tiết
Giải chi tiết giúp mình ạ !
Một học sinh dùng đồng hồ bấm giây đo thời gian rơi tự do của một vật ở độ cao 80cm so với mặt đất. qua 5 lần đo kết quả thu được lần lượt là 0.408; 0.409; 0.409; 0,408; 0,409. Đồng hồ có độ chia nhỏ nhất là 0,001. kết quả đo thời gian rơi tự do được biểu diễn bằng?
Một học sinh dùng đồng hồ bấm dây để đo chu kì dao động điều hào T của một con lắc đơn bằng cách đo thời gian mỗi dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt bằng 2,01 s; 2,12 s; 1,99 s. Thang chia nhỏ nhất của đồng hồ là 0,01 s. Kết quả của phép đo chu kì được biểu diễn bằng A. T (6,12 ± 0,05) s B. T (6,12 ± 0,06) s C. T (2,04 ± 0,05) s D. T (2,04 ± 0,06) s
Đọc tiếp
Một học sinh dùng đồng hồ bấm dây để đo chu kì dao động điều hào T của một con lắc đơn bằng cách đo thời gian mỗi dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt bằng 2,01 s; 2,12 s; 1,99 s. Thang chia nhỏ nhất của đồng hồ là 0,01 s. Kết quả của phép đo chu kì được biểu diễn bằng
A. T = (6,12 ± 0,05) s
B. T = (6,12 ± 0,06) s
C. T = (2,04 ± 0,05) s
D. T = (2,04 ± 0,06) s
Dùng một đồng hồ đo thời gian có độ chia nhỏ nhất 0.001s để đo n lần thời gian rơi tự do của một vật bắt đầu từ điểm A (vA 0) đến điểm B, kết quả cho trong Bảng 7.1.
Hãy tính thời gian rơi trung bình, sai số ngẫu nhiên, sai số dụng cụ và sai số phép đo thời gian: Phép đo này trực tiếp hay gián tiếp? Nếu chỉ đo 3 lần (n 3) thì kết quả đo bằng bao nhiêu?
Đọc tiếp
Dùng một đồng hồ đo thời gian có độ chia nhỏ nhất 0.001s để đo n lần thời gian rơi tự do của một vật bắt đầu từ điểm A (vA = 0) đến điểm B, kết quả cho trong Bảng 7.1.
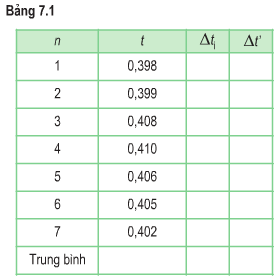
Hãy tính thời gian rơi trung bình, sai số ngẫu nhiên, sai số dụng cụ và sai số phép đo thời gian: Phép đo này trực tiếp hay gián tiếp? Nếu chỉ đo 3 lần (n = 3) thì kết quả đo bằng bao nhiêu?
|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |

Đúng 0
Bình luận (0)
Dùng đồng hồ đo thời gian có độ chia nhỏ nhất đến 0,001 giây để đo 7 lần thời gian rơi tự do của một vật bắt đầu từ điểm A left( {{v_A} 0} right) đến điểm B. Kết quả đo như sau:0,398 0,399 0,408 0,410 0,406 0,405 0,402.(Theo Bài tập Vật lý 10, Nhà xuất bản Giáo dục Việt Nam, 2018)Hãy tính phương sai và độ lệch chuẩn cho mẫu số liệu này. Qua các đại lượng này, em có nhận xét gì về độ chính xác của phép đo trên?
Đọc tiếp
Dùng đồng hồ đo thời gian có độ chia nhỏ nhất đến 0,001 giây để đo 7 lần thời gian rơi tự do của một vật bắt đầu từ điểm A \(\left( {{v_A} = 0} \right)\) đến điểm B. Kết quả đo như sau:
0,398 0,399 0,408 0,410 0,406 0,405 0,402.
(Theo Bài tập Vật lý 10, Nhà xuất bản Giáo dục Việt Nam, 2018)
Hãy tính phương sai và độ lệch chuẩn cho mẫu số liệu này. Qua các đại lượng này, em có nhận xét gì về độ chính xác của phép đo trên?
Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
Ta có bảng sau:
Giá trị | Độ lệch | Bình phương độ lệch |
0,398 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,399 | 0,005 | \(2,{5.10^{ - 5}}\) |
0,408 | 0,004 | \(1,{6.10^{ - 5}}\) |
0,410 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,406 | 0,002 | \(0,{4.10^{ - 5}}\) |
0,405 | 0,001 | \(0,{1.10^{ - 5}}\) |
0,402 | 0,002 | \(0,{4.10^{ - 5}}\) |
Tổng | \(12,{2.10^{ - 5}}\) |
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.
Đúng 0
Bình luận (0)
Một học sinh dùng đồng hồ bấm dây để đo chu kì dao động điều hòa T của một con lắc đơn bằng cách đo thời gian mỗi dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt bằng 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kì được biểu diễn bằng A. T (6,12
±
0,05)s. B. T (6,12
±
0,06)s. C. T (2,04
±
0,05)s. D. T (2,04
±
0,06)s.
Đọc tiếp
Một học sinh dùng đồng hồ bấm dây để đo chu kì dao động điều hòa T của một con lắc đơn bằng cách đo thời gian mỗi dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt bằng 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kì được biểu diễn bằng
A. T = (6,12 ± 0,05)s.
B. T = (6,12 ± 0,06)s.
C. T = (2,04 ± 0,05)s.
D. T = (2,04 ± 0,06)s.
Chọn đáp án C
Giá trị trung bình:
T ¯ = 2 , 01 + 2 , 12 + 1 , 99 3 = 2 , 04 s .
Trung bình sai lệch:
( 2 , 04 − 2 , 01 ) + ( 2 , 04 − 1 , 99 ) + 2 , 04 − 2 , 12 3
= 0 , 05 ( s ) .
Suy ra T = (2,04 ± 0,05) s.
Đúng 0
Bình luận (0)
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi chu kỳ dao động lần lượt là 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng:
Đọc tiếp
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi chu kỳ dao động lần lượt là 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng:
![]()
![]()
![]()
![]()
Đáp án D
Ta có:
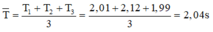
Lại có thêm:
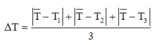
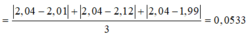
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có:
![]()
Đúng 0
Bình luận (0)
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt là 2,01s; 2,12s; l,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng: A. B. C. D.
Đọc tiếp
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi dao động lần lượt là 2,01s; 2,12s; l,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án D
Ta có:
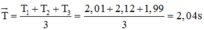
Lại có thêm:
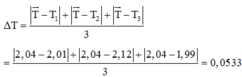
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có: ![]()
STUDY TIP
Áp dụng công thức tính trung bình sẵn có đối với từng
Đúng 0
Bình luận (0)
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi chu kỳ dao động lần lượt là 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng: A.
T
6
,...
Đọc tiếp
Tại một buổi thực hành tại phòng thí nghiệm bộ môn vật lý trường THPT Lương Đắc Bằng. Một học sinh lớp 12A3, dùng đồng hồ bấm giây để đo chu kỳ dao động điều hòa T của một con lắc đơn bằng cách đo thời gian dao động. Ba lần đo cho kết quả thời gian của mỗi chu kỳ dao động lần lượt là 2,01s; 2,12s; 1,99s. Thang chia nhỏ nhất của đồng hồ là 0,01s. Kết quả của phép đo chu kỳ được biểu diễn bằng:
A. T = 6 , 12 ± 0 , 05 s
B. T = 2 , 04 ± 0 , 05 s
C. T = 6 , 12 ± 0 , 06 s
D. T = 2 , 04 ± 0 , 06 s
Đáp án D
Ta có: T ¯ = T 1 + T 2 + T 3 3 = 2 , 01 + 2 , 12 + 1 , 99 3 = 2 , 04 s
Lại có thêm: Δ T = T ¯ − T 1 + T ¯ − T 2 + T ¯ − T 3 3 = 2 , 04 − 2 , 01 + 2 , 04 − 2 , 12 + 2 , 04 − 1 , 99 3 = 0 , 0533
Vì tính thêm cả thang chia nhỏ nhất của đồng hồ nên ta sẽ có: T = 2 , 04 ± 0 , 06 s
Đúng 0
Bình luận (0)










