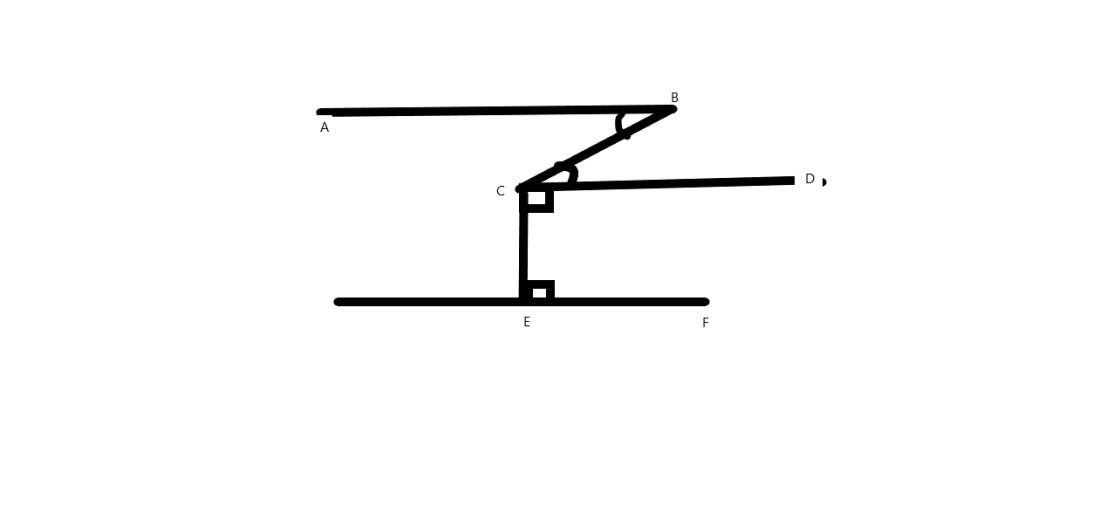
a) chứng minh AB//CD
b) chứng minh AB//EF
Những câu hỏi liên quan
15 tháng 12 2021 lúc 18:17
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
15 tháng 12 2021 lúc 17:07
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.Ai đó giúp e với:((((((((
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
Ai đó giúp e với:((((((((
15 tháng 12 2021 lúc 19:34
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.giúp em với ạ:(((((
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
giúp em với ạ:(((((
15 tháng 12 2021 lúc 19:52
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
a.Xét tam giác ABM và tam giác CDM có :
AB=CD (gt)
BM=MD(cmt)
BD cạnh chung
=> \(\Delta ABM=\Delta CDM\)
b.*AB//CD
Vì \(\Delta ABM=\Delta CDM\) (cmt )
BAM=MCD( 2 góc tương ứng )
=>AB//CD
*AB=CD
Vì \(\Delta ABM=\Delta CDM\left(cmt\right)\)
=>AB=CD ( 2 cạnh tương ứng )
.Câu d.e.f áp dụng lại như vạy , câu g thì mình lười suy nghĩ ^^
Đúng 1
Bình luận (0)
cho hình thang ABCD có đáy là AB. Chứng minh góc ABD= góc CDB và chứng minh góc ACD= góc CAB
Ta có: AB//CD
nên \(\widehat{ABD}=\widehat{CDB}\) và \(\widehat{ACD}=\widehat{CAB}\)
Đúng 1
Bình luận (0)
15 tháng 12 2021 lúc 16:31
BÀI 1.Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
Giúp em với ạ:(( em đag cần gấp:(((
Cho ∆ABC vuông tại A (AB < AC) có AH là đường cao. a) Chứng minh: ∆ABC ~ ∆HAC và CA²=CH . CB. b) Trên tia đối của tia AB lấy điểm D sao cho BCD= 90⁰ . Vẽ AK vuông góc với CD tại K. Chứng minh ∆CHK ~ ∆CDB.
Cho tam giác ABC vuông tại A (AB < AC).Gọi M là trung điểm của AC.Trên tia đối của tia MB lấy điểm D sao cho MD=MB.
a)Chứng minh rằng:AB=CD,AC _|_ CD
b)Chứng minh rằng:AB+BC>2BM
c)Chứng minh rằng:góc CBM < góc ABM
a) Xét ΔAMD và Δ CMB có :
MA = MC ( M là trung điểm của AC )
Góc AMD = góc CMB ( đối đỉnh )
MB = MD ( gt)
=> ΔAMD = Δ CMB ( c.g.c )
=> AD = BC ( 2 cạnh tương ứng )
*Xét Δv ABM và Δv CDM có :
MB = MD ( gt)
Góc AMB = góc CMD ( đối đỉnh )
=> Δ vABM = Δv CDM ( ch - gn)
=> Góc BAM = góc DCM ( 2 góc tương ứng )
mà góc BAM = 90 độ
=> Góc DCM = 90 độ
Đúng 3
Bình luận (0)
a)Xét tam giác ABM và tam giác CBM có:
BM=MD(gt)
góc BMA=góc DMC(đđ)
AM=CM(gt)
Suy ra 2 tam giác này băng nhau(c.g.c)
Suy ra AB=CD(2 cạnh tương ứng)
Đúng 3
Bình luận (0)
Cho hình thang ABCD đáy nhỏ AB, E là trung điểm AD, F là trung điểm BC. Đường thẳng EF cắt BD ở I và cắt AC ở K.
a) Chứng minh EF // AB // DC.
b) Chứng minh BK là đường trung tuyến của ∆ABC.
c) Chứng minh AB = 2EI.
d) Chứng minh EI = KF.
e) Cho AB = 6, CD = 10. Tính IE; KF; IK?
\(a,\left\{{}\begin{matrix}AE=ED\\BF=FC\end{matrix}\right.\Rightarrow EF\) là đtb hthang ABCD
\(\Rightarrow EF=\dfrac{AB+CD}{2};EF//AB//CD\left(đpcm\right)\)
\(b,\left\{{}\begin{matrix}BF=FC\\FK//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow AK=KC\) hay BK là trung tuyến tg ABC
\(c,\left\{{}\begin{matrix}AE=ED\\EI//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow BI=ID\Rightarrow IE\) là đtb tg ABD
\(\Rightarrow IE=\dfrac{1}{2}AB.hay.AB=2IE\)
\(d,\left\{{}\begin{matrix}BF=FC\\AK=KC\end{matrix}\right.\Rightarrow FK\) là đtb tg ABC
\(\Rightarrow FK=\dfrac{1}{2}AB=IE\left(đpcm\right)\)
\(e,\) Ta có \(FK=IE=\dfrac{AB}{2}=3\)
\(KF=EF-EI-FK=\dfrac{AB+CD}{2}-3-3=8-3-3=2\)
Đúng 1
Bình luận (0)