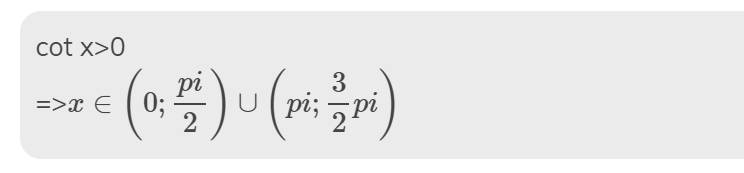 1.17 ạ
1.17 ạ
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
1/1.17+1/2.18+....+1/1984.2000
1.17/25 - 5/41 + 8/25 -36/41 + 1/2
tính nhanh:1.1+1.2.+1.3+1.4+1.5+,...,+1.17+1.18+1.19
So sánh A và B biết :
A = 124.(1/1.1985 + 1/2.1986 + ... + 1/16.2000
B = 1/1.17 + 1/2.18 + 1/3.19 + ... + 1/1984.2000
`Answer:`
\(A=124.\left(\frac{1}{1.1985}+\frac{1}{2.1986}+\frac{1}{3.1987}+...+\frac{1}{16.2000}\right)\)
\(=\frac{124}{1984}.\left(\frac{1984}{1.1985}+\frac{1984}{2.1986}+\frac{1984}{3.1987}+...+\frac{1984}{16.2000}\right)\)
\(=\frac{1}{16}.\left(1-\frac{1}{1985}+\frac{1}{2}-\frac{1}{1986}+\frac{1}{3}-\frac{1}{1987}+...+\frac{1}{16}-\frac{1}{2000}\right)\)
\(=\frac{1}{16}.\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{16}\right)\left(\frac{1}{1985}+\frac{1}{1986}+\frac{1}{1987}+...+\frac{1}{2000}\right)\)
\(B=\frac{1}{1.17}+\frac{1}{2.18}+...+\frac{1}{1984.2000}\)
\(=\frac{1}{16}.\left(\frac{16}{1.17}+\frac{16}{2.18}+...+\frac{16}{1984.2000}\right)\)
\(=\frac{1}{16}.\left(1-\frac{1}{17}+\frac{1}{2}-\frac{1}{18}+...+\frac{1}{1984}-\frac{1}{2000}\right)\)
\(=\frac{1}{16}.\left(1-\frac{1}{17}+\frac{1}{2}-\frac{1}{18}+...+\frac{1}{1984}-\frac{1}{2000}\right)\)
\(=\frac{1}{16}.\left(1+\frac{1}{2}+...+\frac{1}{16}\right)+\left(\frac{1}{17}+\frac{1}{18}+...+\frac{1}{1984}\right)-\left(\frac{1}{17}+\frac{1}{18}+...+\frac{1}{1984}\right)-\left(\frac{1}{1985}+\frac{1}{1986}+...+\frac{1}{2000}\right)\)
\(=\frac{1}{16}.[\left(1+\frac{1}{2}+...+\frac{1}{16}\right)-\left(\frac{1}{1985}+\frac{1}{1986}+...+\frac{1}{2000}\right)]\)
`=>A=B`
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−π2;2π] để hàm số y=cotx nhận giá trị dương.

cot x>0
=>\(x\in\left(0;\dfrac{pi}{2}\right)\cup\left(pi;\dfrac{3}{2}pi\right)\)
Đúng 0
Bình luận (0)
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−\(\dfrac{\pi}{2}\);2π]
để hàm số y=cotx
nhận giá trị dương
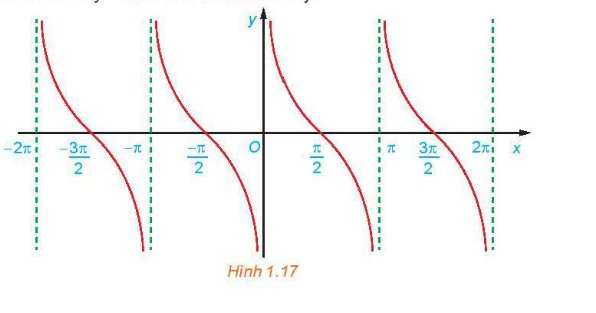
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Đúng 0
Bình luận (0)
Tìm x :
\(\frac{8}{1.9}+\frac{8}{1.17}+...+\frac{8}{49.57}+\frac{58}{57}+2x-2=2x+\frac{7}{3}+5x-\frac{8}{4}\)
Tính nhanh :
\(248.\left(\left(\frac{1}{1.1985}+\frac{1}{2.1984}+....+\frac{1}{16.2000}\right):\left(\frac{1}{1.17}+\frac{1}{2.18}+...+\frac{1}{1984.2000}\right)\right)\)