Chứng tở rằng
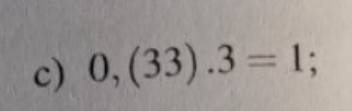
Chứng tở rằng
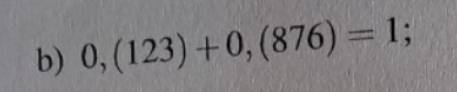
\(0,\left(123\right)+0,\left(876\right)\)
\(=\dfrac{123}{999}+\dfrac{876}{999}\)
\(=\dfrac{123+876}{999}\)
\(=\dfrac{999}{999}\)
\(=1\)
chứng tở rằng
B=4=4^2=4^3+..... +4^45 chia hết cho 21
B=4+42+43+...+445
B=(4+42+43)+...+(443+444+445)
B=4.(4+42+43)+...+443.(4+42+43)
B=4.84+...+443.84
B=84.(4+...+443)
Mà 84 chia hết cho 21 => B chia hết cho 21 (đpcm)
chứng tở rằng
abcabc chia hết cho 7 , 11 , 13
Ta có:
abcabc = 1000abc + abc = 1001.abc
Vì 1001 = 7.11.13 (là tích của 3 số nguyên tố)
=> abcabc luôn chia hết cho 3 số nguyên tố là 7; 11 và 13
abcabc = 1000 x abc + abc
= 1001 x abc = 143 x 7 x abc = 91 x 11 x abc = 77 x 13 x abc
=> abcabc chia hết cho 7, 11, 13
Ta có:
abcabc=abc000 + abc
=abc x1000+abc
=abc x (1000+1)
=abc x 1001
=abc x 7 x 11 x 13
Vì abcabc là tích của 7 x 11x 13 => abcabc chia hết cho 7,11 và 13
cho S= 3/1.4+3/4.7+3/7.10+....+3/40.43+3/43. 46
chứng tở rằng S<1
S = 1 - 1/4 + 1/4 - 1/7 + 1/7 - 1/10 +.............+ 1/40 - 1/43 + 1/43 - 1/46
S = 1 - 1/46
S = 45/46 < 1
=> S < 1 (đpcm)
*** k mk nha các bạn ***
\(s=\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{43.46}\)
\(\Rightarrow s=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+.....+\frac{1}{43}-\frac{1}{46}\)
\(\Rightarrow S=1-\frac{1}{46}=\frac{45}{46}\)
Tao có \(\frac{45}{46}<1\) => S < 1
Cho a,b,c thuộc z . Biết ab - ac + bc - cc = -1
Chứng tở rằng a và b là hai số đối nhau
\(ab-ac+bc-c^2=-1\)
\(a\left(b-c\right)+c\left(b-c\right)=-1\)
\(\left(a+c\right)\left(b-c\right)=-1\)
Vì \(a,b,c\in Z\Rightarrow a+c,b-c\in Z\)
\(\Rightarrow a+c,b-c\inƯ\left(-1\right)\)
*Lập bảng
| a+c | -1 | 1 |
| b-c | 1 | -1 |
| a | -(1+c) | 1-c |
| b | 1+c | -(1-c) |
Vậy nếu ab-ac+bc-c2=-1 thì a và b là 2 số đối nhau
Chứng tở rằng:
1<1/5+1/6+...+1/16+1/1<2
Cho a và b số không dương, chứng tở rằng \(a^3+b^3>ab\left(a+b\right)\)
\(a=b=0\Rightarrow0+0>0\) xem lại đề
Sửa đề: a, b là số âm
c/m \(a^3+b^3>ab\left(a+b\right)\Leftrightarrow ab\left(a+b\right)-\left(a+b\right)\left(a^2-ab+b^2\right)< 0\)
\(\left(a+b\right)\left[ab-\left(a^2-2ab+b^2\right)\right]=-\left(a+b\right)\left(a-b\right)^2>0\) => đề sai
cho s = 1 phần 3 + 1 phần 5 + 1 phần 7 + 1 phần 9 +....+ 1 phần 99+1 phần 101.chứng tở rằng s không phải là số tự nhiên
chứng tở rằng\(\frac{a}{b}<\frac{a+1}{b+1}\) với a;b thuộc Z; a<b; b>0
Ta có: a.(b+1) b.(a+1)
=ab+a = ab +b
Vì a,b thuộc Z và a<b,b>0
suy ra: ab+a < ab+b
suy ra: a/b<a+1/b+1 (ĐPCM)
Xét hiệu : \(a\left(b+1\right)-b\left(a+1\right)=ab+a-ab-b=a-b\)
Vì a<b => a-b<0 => a(b+1) -b(a+1)<0 => a(b+1)<b(a+1)
Mặt khác vì b>0 nên b+1>0 => b(b+1)>0
=> \(\frac{a\left(b+1\right)}{b\left(b+1\right)}< \frac{b\left(a+1\right)}{b\left(b+1\right)}hay\frac{a}{b}< \frac{a+1}{b+1}\)