\(0,\left(123\right)+0,\left(876\right)\)
\(=\dfrac{123}{999}+\dfrac{876}{999}\)
\(=\dfrac{123+876}{999}\)
\(=\dfrac{999}{999}\)
\(=1\)
\(0,\left(123\right)+0,\left(876\right)\)
\(=\dfrac{123}{999}+\dfrac{876}{999}\)
\(=\dfrac{123+876}{999}\)
\(=\dfrac{999}{999}\)
\(=1\)
Chứng tở rằng
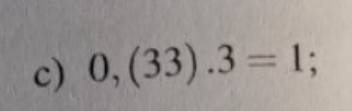
chứng tở rằng\(\frac{a}{b}<\frac{a+1}{b+1}\) với a;b thuộc Z; a<b; b>0
cho A = 1 -2/3 +(2/3)^2-(2/3)^3+.....+ (2/3)^2018-(2/3)^2019 chứng tở A không nguyên
chứng tở rằng :
c) tổng của 2 số tự nhiên liên tiếp thì không chia hết cho 2
d) tổng của 3 số tự nhiên liên tiếp là 1 số chia hết cho 3
e) tổng của 4 số tự nhiên liên tiếp thì không chia hết cho 4
Có 16 tờ giấy bạc loại 2000đ,5000đ và 10000đ. Trị giá mỗi loại tiền trên đều bằng nhau. Hỏi mỗi loại có mấy tở.
cho hai góc kề bù \(\widehat{AOC}\)và \(\widehat{COB}\). gọi OM là tia phân giác của \(\widehat{AOC}\). Vẽ tia ON vuông góc với OM tia (OM nằm trong góc \(\widehat{BOC}\)) chứng tở tia ON là tia phân giác của \(\widehat{BOC}\)
Cho ∆CAM có CA = CM. Gọi I là trung điểm của AM. a) Chứng minh rằng: ∆CIA = ∆CIM. b) Chứng minh rằng: CIA=CIM c) Chứng minh rằng: CI ⊥ AM.
Giúp mình với!
Cho tam giác ABC. Gọi D, E theo thứ tự là trung điểm của AB, AC.
a) Trên tia đối của tia ED lấy điểm I sao cho EI =ED. Chứng minh rằng AI = DC
b) Chứng minh rằng AI // DC
c) Chứng minh rằng tam giác DAI = tam giác BDC
d) Chứng minh rằng DE = 1/2BC, DE // BC
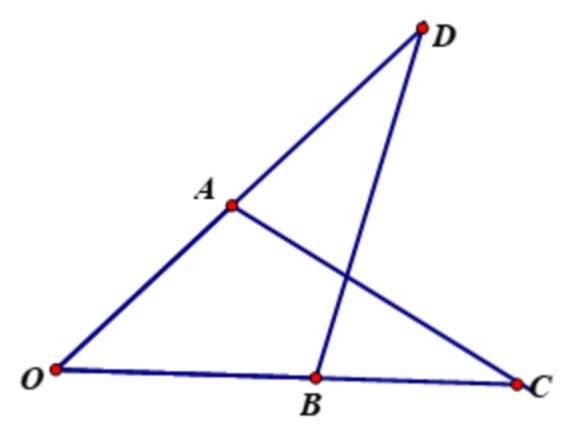
Cho hình vẽ sau, biết OA = OB; góc OAC = góc OBD.
a) Chứng minh rằng AC = BD; OC = OD; AD = BC.
b) Chứng minh rằng tam giác ADC = tam giác BCD.
c) Gọi I là giao điểm của AC và BD. Chứng minh rằng IA = IB và IC = ID.
d) Chứng minh rằng OI là tia phân giác của góc AOB và OI vuông góc CD.