13. Cho tam giác ABC, điểm M trên cạnh BC. Vẽ ME // AB( E ϵ AC); MF // AC( F ϵ AB). Xác định vị trí của điểm M để tia MA là tia phân giác của góc EMF.
Gíup mình với cảm ơn các bạn nhiều!!!
13. Cho tam giác ABC, điểm M trên cạnh BC. Vẽ ME // AB( E ϵ AC); MF // AC( F ϵ AB). Xác định vị trí của điểm M để tia MA là tia phân giác của góc EMF.
Gíup mình với cảm ơn các bạn nhiều!!!
Em nhập lại câu hỏi nha
Cho tam giác ABC, điểm M trên cạnh BC. Vẽ tia ME // AB (E thuộc AC), MF // AC
(F thuộc AB). Xác định vị trí của điểm M để trên tia MA là tia phân giác của góc
EMF ?
Cho tam giác ABC, điểm M trên cạnh BC. Vẽ tia ME // AB (E thuộc AC), MF // AC (F thuộc AB). Xác định vị trí của điểm M để trên tia MA là tia phân giác của góc EMF ?
Cho tam giác ABC. Từ điểm M trên cạnh BC vẽ M D / / A B , M E / / A C D ∈ A C , E ∈ A B . Xác định vị trí của điểm M để tia MA là tia phân giác của góc DME
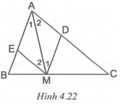
Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A
Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A

Cho tam giác ABC và điểm O nằm trong tam gisc , điểm E nằm trên cạnh AO từ EF//AB (F ϵ BO) ,EH//AC (H ϵ OC) CM rằng FH//BC
Đầu tiên, ta có EF//AB và EH//AC. Theo định lí Thales, khi có hai đường thẳng song song cắt qua các đường thẳng tạo ra các đoạn thẳng có tỉ số bằng nhau, ta có thể kết luận rằng các đoạn thẳng tạo ra bởi các đường thẳng song song đó cũng có tỉ số bằng nhau. Vì vậy, ta có:
EF/AB = EH/AC
Tiếp theo, ta sẽ sử dụng định lí Bồi thường. Theo định lí Bồi thường, khi có hai đường thẳng song song cắt qua một đường thẳng, các đoạn thẳng tạo ra bởi các đường thẳng song song đó và đường thẳng cắt qua có tỉ số bằng nhau, thì các đoạn thẳng tạo ra bởi các đường thẳng song song đó cũng có tỉ số bằng nhau. Vì vậy, ta có:
FH/BC = EH/AC
Vì EF//AB và FH/BC = EH/AC, ta có FH//BC.
Cho tam giác ABC nhọn, M là điểm bất kỳ trên cạnh BC (M khác B;C). Từ M vẽ ME//AC với E thuộc AB, vẽ MF//AB với F thuộc AC. Chứng minh AE.EB + AF.FC > BM.MC
Cho tam giác ABC, trên cạnh BC lấy điểm M. Kẻ MD//AB, ME//AC,( D thuộc AC, E thuộc AB). Vẽ điểm I sao cho DE là đường trung trực của MI. CM: tứ giác AIED là hình thang cân
a) Ta có: \(BC^2=13^2=169\)
\(AB^2+AC^2=5^2+12^2=169\)
Do đó: \(BC^2=AB^2+AC^2\)(=169)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
cho tam giác ABC cân tại A , vẽ BH vuông góc AC tại H . từ điểm M trên cạnh BC , vẽ ME vuông góc AB tại E , MF vuông góc AC tai F . chứng minh BM= ME+ MF