Cho các số hữu tỉ -2/3;-3/5;2/3;5/4;0.Hãy sắp xếp các số hữu tỉ theo thứ tự tăng dần.

Những câu hỏi liên quan
C1: vì s các số 0,6; -1,25; 1/1/3 là các số hữu tỉC2: số nguyên a có phải số hữu tỉ k, vì sC3: biểu diễn các số nguyên: -1;1;2 trên trục sốC4: so sánh 2 ps -2/3;4/-5C5: trong các số hữu tỉ sau số nào là số hữu tỉ âm, số nào là số hữu tỉ dương, số nào k là số hữu tỉ dương cx k phải là số hữu tỉ âm?-3/7;2/3;1/-5;-4;0/-2;-3/-5.ai tl đầy đủ và đúng mk tick cho
Đọc tiếp
C1: vì s các số 0,6; -1,25; 1/1/3 là các số hữu tỉ
C2: số nguyên a có phải số hữu tỉ k, vì s
C3: biểu diễn các số nguyên: -1;1;2 trên trục số
C4: so sánh 2 ps -2/3;4/-5
C5: trong các số hữu tỉ sau số nào là số hữu tỉ âm, số nào là số hữu tỉ dương, số nào k là số hữu tỉ dương cx k phải là số hữu tỉ âm?
-3/7;2/3;1/-5;-4;0/-2;-3/-5.
ai tl đầy đủ và đúng mk tick cho
Trong các số hữu tỉ sau số hữu tỉ nào là dương số hữu tỉ nào là âm số nào ko là số hữu tỉ dương cũng ko phải là số hữu tỉ âm. vì sao
-3/7, 2/3, 1/-5, -4, 0/-2, -3/-5
Các số hữu tỉ âm là :
\(\frac{-3}{7};\frac{1}{-5};-4\)
CÁc số không phải số hữ tỉ âm + giải thích là :
\(\frac{2}{3}>0\)
\(\frac{0}{-2}=0\)( không là số hữu tỉ âm cũng không là số hữu tỉ dương )
\(\frac{-3}{-5}=\frac{3}{5}>0\)
Trong các số sau , số nào là số hữu tỉ dương , số nào là hữu tỉ âm , số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm ; -3/7 ; 2/3 ; -1/5 ; -4 ; 0/-2; -3/5 ;3/0
Số hữu tỷ dương: \(\frac{2}{3}\)Số hữu tỷ âm: \(\frac{-3}{7};\frac{-1}{5};-4;\frac{-3}{5}\)Số không phải số hữu tỷ âm cũng không phải số hữu tỷ dương: \(\frac{0}{-2}\)Số 3/0 không phải là số hữu tỷ.
Đúng 0
Bình luận (0)
cho số thực x thỏa mãn , x + 2/3 và x^5 đều là các số hữu tỉ, chứng minh rắng x là số hữu tỉ
Lời giải:
Đặt $x+\frac{2}{3}=\frac{a}{b}$ với $a,b$ là số nguyên, $b\neq 0$
$\Rightarrow x=\frac{a}{b}-\frac{2}{3}=\frac{3a-2b}{3b}$
Thấy rằng $3a-2b\in\mathbb{Z}$ với mọi $a,b$ nguyên, $3b\in\mathbb{Z}\neq 0$ với mọi số nguyên $b$ khác $0$
$\Rightarrow x$ là số hữu tỉ.
Đúng 0
Bình luận (0)
Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm ?
-
3
7
;
2
3
;
1
5
;
-
4
;
0
-
2
;
...
Đọc tiếp
Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm ?
- 3 7 ; 2 3 ; 1 5 ; - 4 ; 0 - 2 ; - 3 - 5
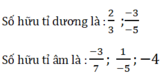
Số hữu tỉ không là số hữu tỉ dương cũng không là số hữu tỉ âm là: 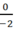
Đúng 0
Bình luận (0)
a) Vì sao các số 0,6; -1,25 là các số hữu tỉ?b) Số nguyên a có là số hữu tỉ không, vì sao?c) Biểu diễn các số nguyên: -1; 1; 2 trên trục số.d) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm? -3 phần 7; 2 phần 3; 1 phần -5; -4; 0 phần -2; -3 phần -5
Đọc tiếp
a) Vì sao các số 0,6; -1,25 là các số hữu tỉ?
b) Số nguyên a có là số hữu tỉ không, vì sao?
c) Biểu diễn các số nguyên: -1; 1; 2 trên trục số.
d) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
-3 phần 7; 2 phần 3; 1 phần -5; -4; 0 phần -2; -3 phần -5
Vì \(0,6=\frac{6}{10}=\frac{3}{5}\)
\(-1,25=\frac{-125}{100}=\frac{-5}{4}\)
nên 0,6 và -1,25 là các số hữu tỉ
Số nguyên a là số hữu tỉ vì ta có thể viết a dưới dạng phân số là \(\frac{\alpha}{1}\)Câu c bạn tự vẽ nhasố hữu tỉ dương : \(\frac{2}{3};\frac{-3}{-5}\)số hữu tỉ âm : \(\frac{-3}{7};\frac{1}{-5};-4\)
số không hữu tỉ âm cũng không phải hữu tỉ dương là \(\frac{0}{-2}\) ( vì kết quả bằng 0 )
Đúng 0
Bình luận (0)
a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
\(\frac{5}{{12}};\, - \frac{4}{5};\,2\frac{2}{3};\, - 2;\,\frac{0}{{234}};\, - 0,32.\)
b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.
a) Các số hữu tỉ dương là: \(\frac{5}{{12}};\,2\frac{2}{3}.\)
Các số hữu tỉ âm là: \( - \frac{4}{5}; - 2;\, - 0,32.\)
Số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{234}}\).
b) Ta có: \( - \frac{4}{5} = -0,8\)
Vì 0 < 0,32 < 0,8 < 2 nên 0 > -0,32 > -0,8 > -2 hay \(-2 < - \frac{4}{5} < -0,32 < 0\)
Mà \(0 < \frac{5}{12} <1; 1<2\frac{2}{3}\) nên \(0 < \frac{5}{12} < 2\frac{2}{3}\)
Các số theo thứ tự từ nhỏ đến lớn là:
\(-2 ; - \frac{4}{5} ; -0,32; \frac{0}{{234}}; \frac{5}{12} ; 2\frac{2}{3}\)
Chú ý: \(\frac{0}{a} = 0\,,\,a \ne 0.\)
Đúng 0
Bình luận (0)
Cho các số hữu tỉ: \(\frac{{ - 7}}{{12}};\,\frac{4}{5};\,5,12;\, - 3;\,\frac{0}{{ - 3}};\, - 3,75.\)
a) So sánh \(\frac{{ - 7}}{{12}}\) với \( - 3,75\); \(\frac{0}{{ - 3}}\) với \(\frac{4}{5}\).
b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
a) +) Ta có: \( - 3,75 = \frac{{ - 375}}{{100}} = \frac{{ - 15}}{4} = \frac{{ - 45}}{{12}}\).
Do \( - 7 > - 45\) nên \(\frac{{ - 7}}{{12}} > \frac{{ - 45}}{{12}}\).
+) Ta có: \(\frac{0}{{ - 3}} = 0\). Nên \(\frac{0}{{ - 3}} < \frac{4}{5}\).
b) Các số hữu tỉ dương là: \(\frac{4}{5};\,5,12\).
Các số hữu tỉ âm là: \(\frac{{ - 7}}{{12}};\, - 3;\, - 3,75\)
Do \(\frac{0}{{ - 3}} = 0\) nên số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{ - 3}}\).
Đúng 0
Bình luận (0)
cho 3 số 9x,4y,\(3\sqrt{x}+2\sqrt{y}\) là các số hữu tỉ. Chứng minh rằng \(\sqrt{x},\sqrt{y}\)là các số hữu tỉ.
Ta có \(9x-4y=\left(3\sqrt{x}-2\sqrt{y}\right)\left(3\sqrt{x}+2\sqrt{y}\right)\)là số hữu tỷ
Vì \(\left(3\sqrt{x}-2\sqrt{y}\right)\)(1) là số hữu tỷ nên \(\left(3\sqrt{x}+2\sqrt{y}\right)\)(2) cũng là số hữu tỷ
Lấy (2) - (1) và (2) + (1) ta được
\(\hept{\begin{cases}4\sqrt{y}\\6\sqrt{x}\end{cases}}\)là 2 số hữu tỷ vậy \(\sqrt{x},\sqrt{y}\)là hai số hữu tỷ
Đúng 0
Bình luận (0)

















