y'yBDACMFE

a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.

c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE

a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.

c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE.

a) -  \(MA.MB=MC.MD\left(gt\right)\Rightarrow\dfrac{MA}{MD}=\dfrac{MC}{MB}\)

-  \(\Delta MAC\) và \(\Delta MBD\)  có:

\(\dfrac{MA}{MD}=\dfrac{MC}{MB}\left(cmt\right)\)

\(\widehat{M_1}=\widehat{M_2}\)   (đối đỉnh)

=> \(\Delta MAC\sim\Delta MDB\)  (c-g-c)

\(\Rightarrow\widehat{A_1}=\widehat{D_2}\) ( góc tương ứng)  (1)

-  \(MA.MB=MC.MD\left(gt\right)\Rightarrow\dfrac{MA}{MC}=\dfrac{MD}{MB}\)

-  \(\Delta MBC\) và \(\Delta MAD\) có:

\(\dfrac{MA}{MC}=\dfrac{MD}{MB}\left(cmt\right)\)  

\(\widehat{M_3}=\widehat{M_4}\)  (đối đỉnh)

=> \(\Delta MCB\sim\Delta MAD\)  (c-g-c)

=> \(\widehat{A_2}=\widehat{C_1}\) (góc tương ứng)  (2)

\(\Delta BCD,\widehat{C_1}+\widehat{D_2}+\widehat{CBD}=180^0\) (tổng 3 góc tam giác) (3)

- Từ (1) (2) và (3) => \(\widehat{A_1}+\widehat{A_2}+\widehat{CBD}=180^0\) hay \(\widehat{CAD}+\widehat{CBD}=180^0\)

=> A, B,C,D cùng thuộc 1 đường tròn ( dấu hiệu nhận biết tứ giác nội tiếp)

b) \(MD.ME=MB.MF\Rightarrow\dfrac{MD}{MF}=\dfrac{MB}{ME}\)

\(\Delta MDB\)  và  \(\Delta MEF\)  có:

\(\dfrac{MD}{MF}=\dfrac{MB}{ME}\left(cmt\right)\)

\(\widehat{M_2}\) chung

=> \(\Delta MDB\sim\Delta MFE\) (c-g-c)

=> \(\widehat{D_2}=\widehat{F_1}\) (góc tương ứng)

mà \(\widehat{D_2}+\widehat{D_3}=180^0\)  (kề bù)

=> \(\widehat{F_1}+\widehat{D_3}=180^0\)

=> B,D,E,F cùng thuộc 1 đường tròn ( dấu hiệu nhận biết tứ giác nội tiếp)

c)  \(\widehat{A_1}=\widehat{D_2}(\Delta MAC\sim\Delta MDB)\left(1\right)\)  

mà \(\widehat{D_2}=\widehat{F_1}\left(cmt\right)\left(2\right)\)  

Từ (1) (2) => \(\widehat{A_1}=\widehat{F_1}\)  

mà \(\widehat{A_1}\)  và \(\widehat{F_1}\) so le trong 

=> AC // EF 

gọi I là giao điểm của MF và NE

Xét \(\Delta MIN\) có : \(MN< MI+NI\) ( tổng hai cạnh lớn hơn một cạnh ) (1)

Xét \(\Delta EIF\) có : \(EF< FI+EI\) (tổng hai cạnh lớn hơn một cạnh ) (2)

Từ (1 ) và (2) \(\Rightarrow MN+EF< MI+NI+EI+FI\)

\(\Rightarrow MN+EF< MF+NE\left(đpcm\right)\)

Gọi I là giao điểm của MF và NE

Xét \(\Delta MIN\) có :MN < MI + NI (tổng 2 cạnh lớn hơn 1 cạnh )(1)

Xét \(\Delta EIF\) có : EF < FI + EI (tổng 2 cạnh lớn hơn 1 cạnh)(2)

Từ (1) và (2) ta được :

MN + EF < MI + NI + EI +FI

\(\Rightarrow\) MN + EF < MF + NE (đpcm)

Sửa đề:

Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:

a) Tứ giác MQFE là hình bình hành

b) Trung điểm của MF thuộc đường thẳng QE

GIẢI 

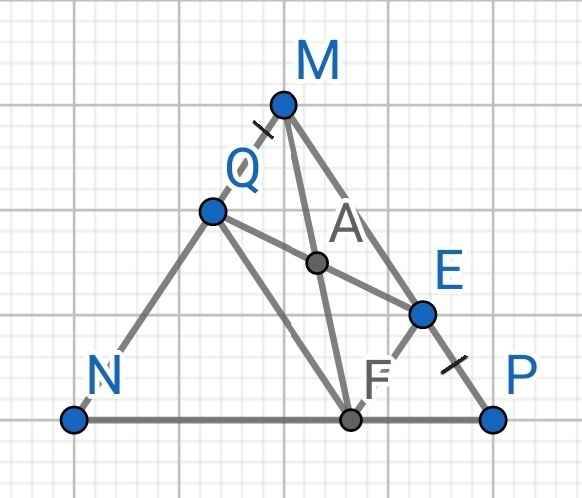
a) Do ∆MNP cân tại M (gt)

⇒ MN = MP

Mà MQ = PE (gt)

⇒ MN - MQ = MP - ME

⇒ QN = ME

Do QF // MP (gt)

⇒ ∠QFN = ∠MPN (đồng vị) (1)

Mà ∆MNP cân tại M

⇒ ∠MPN = ∠MNP

⇒ ∠MPN = ∠QNF (2)

Từ (1) và (2) ⇒ ∠QFN = ∠QNF

⇒ ∆QNF cân tại Q

⇒ QN = QF

Mà QN = ME (cmt)

⇒ QF = ME

Do QF // MP (gt)

⇒ QF // ME

Tứ giác MQFE có:

QF // ME (cmt)

QF = ME (cmt)

⇒ MQFE là hình bình hành

b) Gọi A là trung điểm của MF

Do MQFE là hình bình hành

⇒ A là trung điểm của hai đường chéo MF và QE

⇒ A là trung điểm của QE

⇒ A ∈ QE

Bài 2: 

a: Trên tia Ox, ta có: OE<OF

nên điểm E nằm giữa hai điểm O và F

b: Vì E nằm giữa O và F

mà OE=1/2OF

nên E là trung điểm của OF