đó là hình bình hành đó bạn ơi. 
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1) 
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2) 
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một) 
Chúc bạn thành công...

tk nha bạn

thank you bạn

a, Ta noi AC lai voi nhau .

Xet tam giac ABD co :

AH=HD a AE=EB

=> HE la dtb => HE=1/2BD va HE//DB (1)

Xet tam giac BDC co : 

DG=GC va BF=FC

=> GF la dtb => GF=1/2BD va GF//BD (2)

Tu (1) va (2) suy ra : HE//GF va HE=GF

Hay tứ giác EFGH la HBH

b, Nếu AC vuông góc với BD thì tứ giác EFGH là hình HCN vì :

Ta có : AC//EF va BD//HE

=> E=90

Hay hình bình hành EFGH là hình chữ nhật ( hình bình hành có 1 góc vuông là hình chữ nhật)

c, Áp dụng định lý pi-ta-go là : 

AO²+OB²=AB²

x²+8²=10²

x²=10²-8²

x²=36

=>x=6

Dien h tam giac AOB la : 

\(\frac{1}{2}.6.8=24cm^2\)

Vay dien h tam giac AOB la 24cm²

Câu a bạn có thể kham khảo bài của bạn le anh tu (co 2 cach)

nho k nha

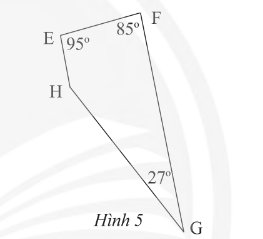
a) Ta có:

\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ  + 85^\circ  = 180^\circ \)

Mà hai góc ở vị trí Trong cùng phía

Suy ra \(EH\;{\rm{//}}\;FG\)

Suy ra: \(EFGH\) là hình thang

b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)

\(\begin{array}{l}95^\circ  + 85^\circ  + 27^\circ  + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)

a) Xét ΔABC có

E là trung điểm của AB(gt)

F là trung điểm của BC(gt)

Do đó: EF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

⇒EF//AC và \(EF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)

Xét ΔADC có

H là trung điểm của AD(gt)

G là trung điểm của CD(gt)

Do đó: HG là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)

⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)

Từ (1) và (2) suy ra HG//EF và HG=EF

Xét ΔABD có 

E là trung điểm của AB(gt)

H là trung điểm của AD(gt)

Do đó: EH là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)

⇒EH//BD và \(EH=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)

Ta có: EH//BD(cmt)

BD⊥AC(gt)

Do đó: EH⊥AC(Định lí 2 từ vuông góc tới song song)

Ta có: HG//AC(cmt)

EH⊥AC(Cmt)

Do đó: HG⊥HE(Định lí 2 từ vuông góc tới song song)

hay \(\widehat{EHG}=90^0\)

Xét tứ giác EHGF có 

HG//EF(cmt)

HG=FE(cmt)

Do đó: EHGF là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Hình bình hành EHGF có \(\widehat{EHG}=90^0\)(cmt)

nên EHGF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

b) Ta có: EFGH là hình chữ nhật(cmt)

nên \(S_{EFGH}=EF\cdot EH\)

\(\Leftrightarrow S_{EFGH}=\dfrac{AC}{2}\cdot\dfrac{BD}{2}=\dfrac{10}{2}\cdot\dfrac{8}{2}=5\cdot4=20cm^2\)

Vậy: Diện tích tứ giác EFGH khi AC=10cm và BD=8cm là 20cm²

c) Hình chữ nhật EFGH trở thành hình vuông khi EH=HG

hay AC=BD

Vậy: Khi tứ giác ABCD có thêm điều kiện AC=BD thì EFGH trở thành hình vuông

a: Xét ΔABD có 

E là trung điểm của AB

H là trung điểm của AD

Do đó: EH là đường trung bình

=>EH//BD và EH=BD/2(1)

Xét ΔBCD có 

F là tđiểm của BC

G là tđiểm của CD

Do đó: FG là đường trung bình

=>FG//BD và FG=BD/2(2)

Xét ΔADC có 

H là tđiểm của AD

G là tđiểm của CD

Do đó: GH là đường trung bình

=>GH⊥EH(3)

Từ (1), (2) và (3) suy ra EFGH là hình chữ nhật

Bổ sung: \(EF//GH;EF=GH\)

EF//GH; EF=GH

không có hình kìa

làm sao mà trả lời được

b: Xét tứ giác EBFD có 

ED//BF

ED=BF

Do đó: EBFD là hình bình hành

ΔDFG= ΔCHG(GD=GC;DF=CH;góc FDG=gócHCG)
=>GF=GH(1)
 ΔEFB= ΔEHA(FB=HA;EB=EA;gócEAH=gócABF)
=>EF=EH(2)
TỪ 1 và 2=> tứ giác EFGH là hình thoi

a: Xét ΔABC có 

E là trung điểm của AB

H là trung điểm của AC

Do đó: EH là đường trung bình của ΔABC

Suy ra: EH//BC và EH=BC/2(1)

Xét ΔBDC có 

F là trung điểm của BD

G là trung điểm của CD

Do đó: FG là đường trung bình của ΔBDC

Suy ra: FG//BC và FG=BC/2(2)

Xét ΔABD có 

E là trung điểm của AB

F là trung điểm của BD

Do đó: EF là đường trung bình của ΔABD

Suy ra: EF//AD và EF=AD/2

hay EF=BC/2(3)

Từ (1) và (2) suy ra EH//FG và EH=FG

Từ (2) và (3) suy ra EF=FG

Xét tứ giác EHGF có

EH//FG

EH=FG

Do đó: EHGF là hình bình hành

mà EF=FG

nên EHGF là hình thoi