Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
A. 7.
B. 7,6.
C. 8.
D. 8,6.
Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
A. 10.
B. 11.
C. 12.
D. 13.
Gọi \({x_1};{x_2};...;{x_{20}}\) là doanh thu bán hàng của các ngày được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2} \in \begin{array}{*{20}{c}}{\left[ {5;7} \right)}\end{array};{x_3},...,{x_9} \in \begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array};{x_{10}},...,{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array};{x_{17}},{x_{18}},{x_{19}} \in \begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array};{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array}\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 7;C = 2 + 7 = 9;{u_j} = 9;{u_{j + 1}} = 11\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 9 + \frac{{\frac{{3.20}}{4} - 9}}{7}.\left( {11 - 9} \right) \approx 10,7\)
Chọn B.
Một mẫu số liệu có tử phân vị thứ nhất là 56 và tứ phân vị thứ ba là 84. Hãy kiểm tra xem trong hai giá trị 10 và 100 giá trị nào được xem là giá trị bất thường.
Ta có \({Q_1} = 56;{Q_3} = 84\)
\({\Delta _Q} = {Q_3} - {Q_1} = 84 - 56 = 28\)
\({Q_1} - 1,5{\Delta _Q} = 56 - 1,5.28 = 14\)
\({Q_3} + 1,5.{\Delta _Q} = 84 - 1,5.28 = 126\)
Ta thấy 10 < 14 nên 10 là giá trị bất thường
Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:
2 5 16 8 7 9 10 12 14 11 6 (1)
a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu đó. Sau đó, tìm hiệu \({Q_3} - {Q_1}\)
a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)
Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:
a) Nhân mỗi giá trị của mẫu số liệu với 2.
b) Cộng mỗi giá trị của mẫu số liệu với 2.
Tham khảo:
n=10
Giả sử sau khi sắp xếp 10 số dương theo thứ tự không giảm thì được:

=> Trung vị là giá trị trung bình của số thứ 5 và thứ 6.
=> \({Q_1}\) là số thứ 3 và \({Q_3}\) là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì:
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần
=> R tăng 2 lần
+ \({Q_1}\) và \({Q_3}\) tăng 2 lần
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) tăng 2 lần.
+ Giá trị trung bình tăng 2 lần
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) cũng tăng 2 lần
=> \({\left( {{x_i} - \overline x} \right)^2}\) tăng 4 lần
=> Phương sai tăng 4 lần
=> Độ lệch chuẩn tăng 2 lần.
Vậy R tăng 2 lần, khoảng tứ phân vị tăng 2 lần và độ lệch chuẩn tăng 2 lần.
b) Cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị
=> R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ \({Q_1}\) và \({Q_3}\) tăng 2 đơn vị
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
=> \({\left( {{x_i} - \overline x} \right)^2}\) không đổi
=> Phương sai không đổi.
=> Độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.
Số trung bình của dãy số liệu 1;1;2;3;3;4;5;6;7;8;9;9;9 gần đúng với giá trị nào nhất trong các giá trị sau?
A. 5,14
B. 5,15
C. 5
D. 6
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 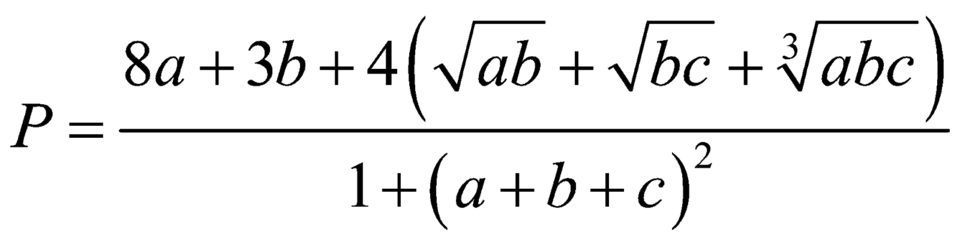 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 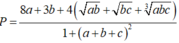 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
Cho mẫu số liệu gồm bốn số tự nhiên khác nhau và khác 0, biết số trung bình là 6 và số trung vị là 5. Tìm các giá trị của mẫu số liệu đó sao cho hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
A. 3;4;6;11
B. 2;4;7;11
C. 3;5;6;11
D. 2;4;6;12
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có 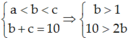 hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
Bảng sau thống kê số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam.

(Nguồn: worldometers.info)
a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?
b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.
Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
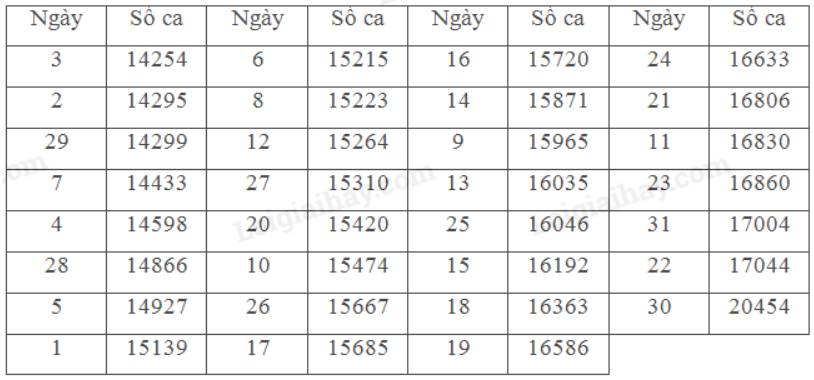
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)

c) Ta có:

• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)