Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các đường thẳng song song trong thực tế.

Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các mặt phẳng song song trong thực tế

a: Các tấm pin năng lượng mặt trời song song với nhau
b: Các bức tường đối diện nhau của toà nhà song song với nhau
Các ví dụ khác: Các bậc cầu thang, mặt bàn và mặt phẳng sàn nhà
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

-Hai thanh sắt đối diện nhau ở hai bên cầu song song với nhau.
-Hai thanh sắt liền nhau cùng nằm ở thành cầu hoặc mái cầu cắt nhau.
-Thanh sắt nằm ở mái cầu và thanh sắt nằm ở thành cầu chéo nhau.
Tìm trên hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1 một ví dụ để chứng tỏ các mệnh để sau đây là sai
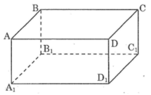
Nếu một đường thẳng cắt một trong hai đường thẳng song song thì cũng cắt đường thẳng kia.
Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a) sai.
Tìm trong thực tế các hình ảnh gợi về:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau
a) có những hình ảnh như : đường cao tốc nhìn từ trên cao ,vạch kẻ trên phần đường dành cho người đi bộ ,....
b) các dây nối của 1 cây cầu
HT
Tìm trong hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1 một ví dụ cụ thể để chứng tỏ phát biểu sau đây là sai. Hai đường thẳng nằm trong hai mặt phẳng song song thì song song với nhau.
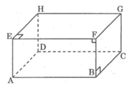
Xét hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1
Ta có: mp(ABCD) // mp( A 1 B 1 C 1 D 1 )
AB thuộc mp(ABCD)
A 1 D 1 thuộc mp( A 1 B 1 C 1 D 1 )
AB không song song với A 1 D 1
Vậy mệnh đề đã cho sai
Tìm trong thực tế hình ảnh các loại góc đã học và hình ảnh hai đường thẳng vuông góc, hai đường song song.

Tham khảo:
Hình ảnh về góc:

Hình ảnh về hai đường thẳng vuông góc:

Hình ảnh về hai đường thẳng song song:

hãy tìm hình ảnh thực tế về 2 đường thẳng song song, khác, tia
Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.
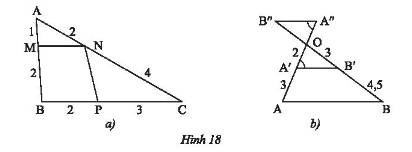
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).
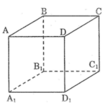
Tìm trên hình hộp chữ nhật \(ABCD.A_1B_1C_1D_1\) (h.101) một ví dụ cụ thể để chứng tỏ các mệnh đề sau đây là sai :
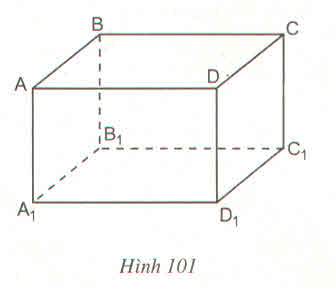
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì cũng cắt đường thẳng kia
b) Hai đường thẳng song song khi chúng không có điểm chung
a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.