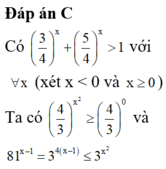với x;y là số nguyên dương tm:\(\frac{x^2-1}{2}=\frac{y^2-1}{3}\). Chứng minh: x^2-y^2 chia hết cho 40. Gjup mk vs mấy bạn nhé. cảm ơn nkju

Những câu hỏi liên quan
Khoanh tròn vào chữ cái trước khẳng định đúng.Bỏ dấu giá trị tuyệt đối của biểu thức |x−2| ta được biểu thức:A. x – 2 với x 2 và 2 – x với x 2B. x – 2 với x
≥
2 và 2 – x với x 2C. x – 2 với x 0 và 2 – x với x 0D. x – 2 với x
≥
0 và 2 – x với x 0
Đọc tiếp
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |x−2| ta được biểu thức:
A. x – 2 với x > 2 và 2 – x với x < 2
B. x – 2 với x ≥ 2 và 2 – x với x < 2
C. x – 2 với x > 0 và 2 – x với x < 0
D. x – 2 với x ≥ 0 và 2 – x với x < 0
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |−5x| ta được biểu thức:
A. -5x với x > 0 và 5x với x < 0
B. -5x với x ≥ 0 và 5x với x < 0
C. 5x với x > 0 và -5x với x < 0
D. -5x với x ≤ 0 và 5x với x > 0
Tìm các số nguyên x biết
a) |x-1| = 6 với x > 1
b) |x+2| = 3 với x > 0
c) x + |3 - x| = 7 với x > 3
a) |x-1| = 6 với x > 1
Do x > 1 nên x + 1 > 0. Từ đó | x - 1| = x – 1 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x – 1 = 6 hay x = 7
b) |x+2| = 3 với x > 0
Do x > 0 nên x + 2 > 0. Từ đó b) |x + 2| = x + 2 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x + 2 = 3 hay x =1
c) x + |3 - x| = 7 với x > 3
Do x > 3 nên 3 - x là một nguyên âm. Từ đó |3 - x| = - (3 - x)
Theo đề bài, ta có:
x + |3 - x| = 7
x + x - 3 = 7
x\(^2\) = 7 + 3 = 10
x = 10 : 2 = 5
Đúng 2
Bình luận (0)
Giải:
a)
|x-1| = 6 với x > 1
Do x > 1 nên x + 1 > 0. Từ đó | x - 1| = x – 1 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x – 1 = 6 hay x = 7
b) |x+2| = 3 với x > 0
Do x > 0 nên x + 2 > 0. Từ đó b) |x + 2| = x + 2 (Giá trị tuyệt đối của một số nguyên dương)
Theo đề bài, ta có: x + 2 = 3 hay x =1
c) x + |3 - x| = 7 với x > 3
Do x > 3 nên 3 - x là một nguyên âm. Từ đó |3 - x| = - (3 - x)
Theo đề bài, ta có:
x + |3 - x| = 7
x + x - 3 = 7
x2 = 7 + 3 = 10
x =10:2=5
Đúng 0
Bình luận (3)
1) x+(16/x-2) với x>2
2) 5x+ (180/x-1) với x>1
3) x/2 +(2x/x-1) với x >1
4) 2/2-x +(1/x) với 0<x<2
Giúp mình với. đề là tìm gtnn
Có bao nhiêu mệnh đề dưới đây là đúng?
3
x
2
x
v
ớ
i
∀
x
∈
ℝ
4
x
2
≥
3
x
2
v
ớ
i
∀
x
∈
ℝ
81
x
-
1
≤
3
x...
Đọc tiếp
Có bao nhiêu mệnh đề dưới đây là đúng?
3 x > 2 x v ớ i ∀ x ∈ ℝ 4 x 2 ≥ 3 x 2 v ớ i ∀ x ∈ ℝ 81 x - 1 ≤ 3 x 2 v ớ i ∀ x ∈ ℝ 5 x + 3 x > 4 x v ớ i ∀ x ∈ ℝ 2 x + 3 x < 5 x v ớ i ∀ x > 1
A. 2
B. 3
C. 4
D. 5
Bỏ dấu GTTĐ
a) /x/ với x > 0
b) /x/ với x < 0
c) / x + 1 / với x > 0
d) / x - 3 / với x > 3
e) / x - 5 / với x < 5
g) / x + 2 / với x < -2
cho x và y tỉ lệ nghịch với nhau với x=5 , y = 1/2 . Tìm h có hệ số tỉ lệ của y với x , biểu diên x theo y , y theo x, với x=-3 . tìm y , với y = -6 tìm x
a: Vì x và y tỉ lệ nghịch
nên hệ số tỉ lệ của y đối với x là \(h=x\cdot y=5\cdot\dfrac{1}{2}=\dfrac{5}{2}\)
b:\(x\cdot y=\dfrac{5}{2}\)
=>\(y=\dfrac{5}{2x};x=\dfrac{5}{2y}\)
Khi x=-3 thì \(y=\dfrac{5}{2\cdot\left(-3\right)}=\dfrac{5}{-6}=-\dfrac{5}{6}\)
Khi y=-6 thì \(x=\dfrac{5}{2\cdot\left(-6\right)}=\dfrac{5}{-12}=-\dfrac{5}{12}\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của các biểu thức sau:a Adfrac{x^3+2021}{x} với x0b B4x+dfrac{25}{x-1}với x1c Cdfrac{3x^4+16}{x^3}với x0d Dx+dfrac{1}{x}với x lớn hơn bằng 2e Edfrac{9x}{2-x}+dfrac{2}{x}với 0x2f Fdfrac{3}{1-x}+dfrac{4}{x}với 0x1
Đọc tiếp
tìm giá trị nhỏ nhất của các biểu thức sau:
a A=\(\dfrac{x^3+2021}{x}\) với x>0
b B=\(4x+\dfrac{25}{x-1}\)với x>1
c C=\(\dfrac{3x^4+16}{x^3}\)với x>0
d D=\(x+\dfrac{1}{x}\)với x lớn hơn bằng 2
e E=\(\dfrac{9x}{2-x}+\dfrac{2}{x}\)với 0<x<2
f F=\(\dfrac{3}{1-x}+\dfrac{4}{x}\)với 0<x<1
a.
\(A=x^2+\dfrac{2021}{x}=x^2+\dfrac{2021}{2x}+\dfrac{2021}{2x}\ge3\sqrt[3]{\dfrac{2021^2}{4x^2}}=3\sqrt[3]{\dfrac{2021^2}{4}}\)
Dấu "=" xảy ra khi \(x=\sqrt[3]{\dfrac{2021}{3}}\)
b.
\(B=4\left(x-1\right)+\dfrac{25}{x-1}+4\ge2\sqrt{\dfrac{100\left(x-1\right)}{x-1}}+4=24\)
Dấu "=" xảy ra khi \(x=\dfrac{7}{2}\)
c.
\(C=3x+\dfrac{16}{x^3}=x+x+x+\dfrac{16}{x^3}\ge4\sqrt[4]{\dfrac{16x^3}{x^3}}=8\)
\(A_{min}=8\) khi \(x=2\)
Đúng 0
Bình luận (0)
d.
\(D=x+\dfrac{1}{x}=\left(\dfrac{x}{4}+\dfrac{1}{x}\right)+\dfrac{3}{4}.x\ge2\sqrt{\dfrac{x}{4x}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=2\)
e.
\(E=\dfrac{9\left(x-2\right)+18}{2-x}+\dfrac{2}{x}=2\left(\dfrac{1}{x}+\dfrac{9}{2-x}\right)-9\ge\dfrac{2.\left(1+3\right)^2}{x+2-x}-9=7\)
\(E_{min}=7\) khi \(x=\dfrac{1}{5}\)
f.
\(F=\dfrac{3}{1-x}+\dfrac{4}{x}\ge\dfrac{\left(\sqrt{3}+2\right)^2}{1-x+x}=7+4\sqrt{3}\)
Dấu "=" xảy ra khi \(x=4-2\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho hàm số :
f
x
x
2
x
v
ớ
i
x
1
,
x
≠
0...
Đọc tiếp
Cho hàm số : f x = x 2 x v ớ i x < 1 , x ≠ 0 0 v ớ i x = 0 x v ớ i x ≥ 1
A. Mọi điểm thuộc R
B. Mọi điểm trừ x=0
C. Mọi điểm trừ x=1
D. Mọi điểm trừ x=0 và x=1
Tính giá trị của (x2-5)(x+3)+(x+4)(x+x2)
a)Với x=0
b)Với x=15
c)Với x=-15
d)Với x=0,15