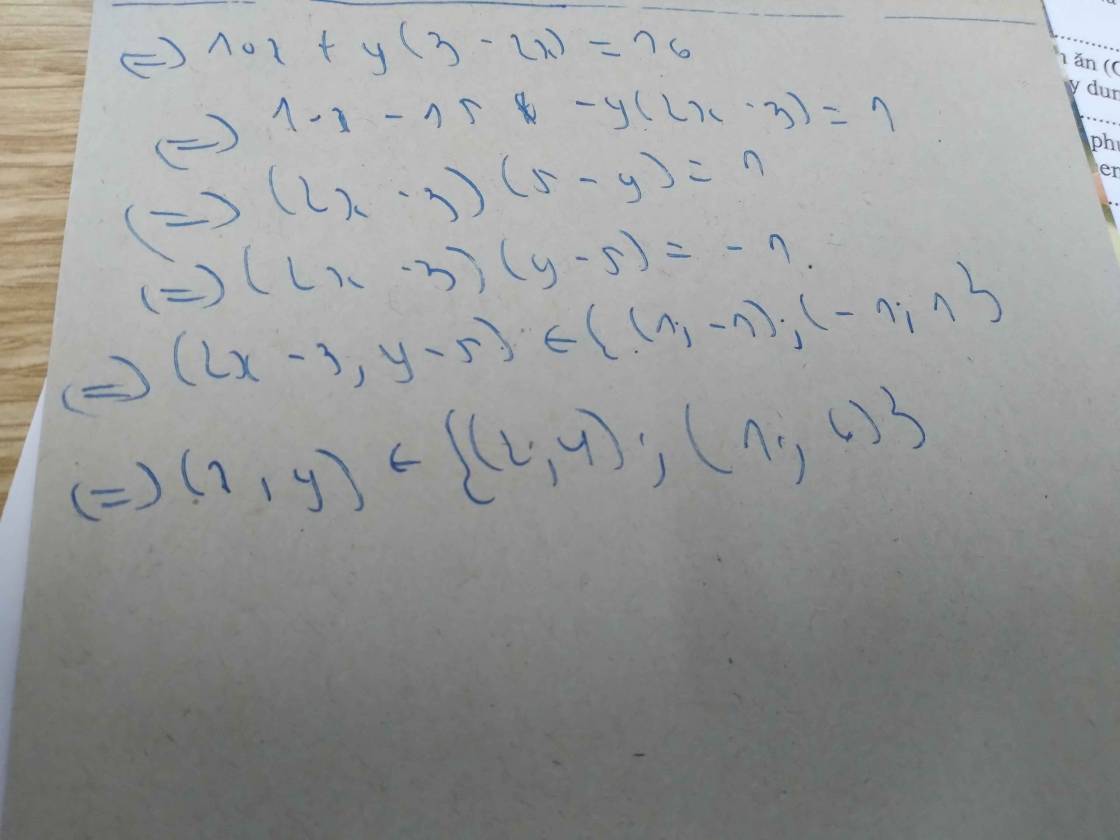tìm số nguyên x,y biết 10x+3y-2xy=16

Những câu hỏi liên quan
tìm số nguyên x,y biết 10x+3y-2xy=16
tìm GTNN, GTLN của S=x+y biết x^2 + 3y^2 + 2xy - 10x - 14y + 18 = 0
Làm nốt phần còn lại của bạn Thắng
(x + y - 5)2 + 2(y - 1)2 - 9 = 0
<=> 2(y - 1)2 = 9 - (S - 5)2 \(\ge0\)
\(\Leftrightarrow\left(S-5\right)^2\le9\)
\(\Leftrightarrow-3\le S-5\le3\)
\(\Leftrightarrow2\le S\le8\)
Vậy GTNN là 2 đạt được khi x = y = 1
GTLN là 8 đạt được khi (x, y) = (7, 1)
Đúng 0
Bình luận (0)
\(x^2+3y^2+2xy-10x-14y+18\)
\(\Rightarrow\left(x^2+2xy-10x+y^2-10y+25\right)+2y^2-4y-7=0\)
\(\Rightarrow\left(x+y-5\right)^2+2y^2-4y+2-9=0\)
\(\Rightarrow\left(x+y-5\right)^2+2\left(y^2-2y+1\right)-9=0\)
\(\Rightarrow\left(x+y-5\right)^2+2\left(y-1\right)^2-9=0\)
....
Đúng 0
Bình luận (0)
x=7;y=±1 và x=y=1 và x=1; y=3 và x=y=3 và x=5;y=-1
Đúng 0
Bình luận (0)
tìm số nguyên dương x,y biết 2xy+x-3y=3
Tìm x,y là số nguyên biết 6xy-10x-3y-4=0
Tìm x,y biết:
a,2x^2+y^2+2xy+10x+25=0
b,x^2+3y^2+2xy-2y+1=0
c,x^2+2y^2+2xy-2x+2=0
a) \(2x^2+y^2+2xy+10x+25=0\)
\(\Leftrightarrow x^2+x^2+y^2+2xy+10x+25=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(x^2+10x+25\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+5\right)^2=0\)
Vì \(\hept{\begin{cases}\left(x+y\right)^2\ge0\forall x\\\left(x+5\right)^2\ge0\forall x\end{cases}}\)
\(\Rightarrow\left(x+y\right)^2+\left(x+5\right)^2\ge0\forall x\)
Vậy đẳng thức xảy ra\(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=5\end{cases}}\)
Đúng 0
Bình luận (0)
b)\(x^2+3y^2+2xy-2y+1=0\)
\(\Leftrightarrow x^2+y^2+2y^2+2xy-2y+\frac{1}{2}+\frac{1}{2}=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(2y^2-2y+\frac{1}{2}\right)+\frac{1}{2}=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}=0\)
Vì \(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2\ge0\)
nên \(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}>0\)
Mà\(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}=0\)
nên pt vô nghiệm
Đúng 0
Bình luận (0)
a) 2x2 + y2 + 2xy + 10x + 25 = 0
=> (x2 + 2xy + y2) + (x2 + 10x + 25) = 0
=> (x + y)2 + (x + 5)2 = 0
<=> \(\hept{\begin{cases}x+y=0\\x+5=0\end{cases}}\) <=> \(\hept{\begin{cases}y=-x\\x=-5\end{cases}}\) <=> \(\hept{\begin{cases}y=5\\x=-5\end{cases}}\)
b)c) xem lại đề
Đúng 0
Bình luận (0)
Tìm số nguyên x, y biết 2xy + 3y - 2x - 2 = -5
2xy + 3y - 2x - 2 = -5
=> 2x(y - 1) + 3y - 3 = -6
=> 2x(y - 1) + 3(y - 1) = -6
=> (2x + 3)(y - 1) = -6
| 2x+3 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| y-1 | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
| x | -1 | -2 | -1/2 | -5/2 | 0 | -3 | 3/2 | -9/2 |
| y | 7 | -5 | 4 | -2 | 3 | -1 | 2 | 0 |
mà x;y nguyên
=> ta có các cặp số (x;y) thỏa mãn là : (-1;7); (-2;5); (0;3); (-3;-1)
tìm x ,y biết : 2xy - 10x + 3y = 33
Ai làm đc gọi bằng thánh
Thêm cho cái điều kiện x,y nguyên.
Ta có:\(2xy-10x+3y=33\)
\(\Rightarrow2x\left(y-5\right)+3\left(y-5\right)=33-15\)
\(\Rightarrow\left(y-5\right)\left(2x+3\right)=18\)
Làm nốt.
Đúng 0
Bình luận (0)
\(2xy-10x+3y=33\)
\(\Leftrightarrow2x\left(y-5\right)+3\left(y-5\right)+15-33=0\)
\(\Leftrightarrow\left(y-5\right)\left(2x+3\right)-18=0\)
\(\Leftrightarrow\left(y-5\right)\left(2x+3\right)=18\)
Lập bảng xét giá trị là xong
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm số nguyên dương x,y biết: 2xy+x-3y=3
Tìm các số nguyên x,y biết ; 2xy+x^2+3y-3xy-3x=0