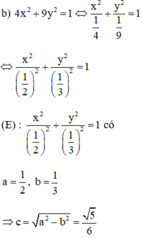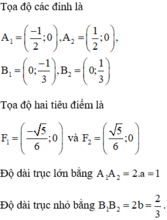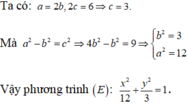Cho elip (E): 4x2 + 25y2 = 36. Xác định độ dài tiêu cự của elip đã cho?
Những câu hỏi liên quan
Xác định độ dài các trục, tọa độ các tiêu điểm, tọa độ các đỉnh của elip có phương trình sau: 4 x 2 + 9 y 2 = 36
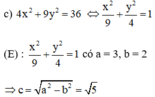
Tọa độ các đỉnh là : A1 = (–3 ; 0) ; A2 = (3 ; 0) ; B1 = (0 ; –2) ; B2 = (0 ; 2)
Tọa độ hai tiêu điểm là F1 = (–√5 ; 0) và F2 = (√5 ; 0)
Độ dài trục lớn là A1A2 = 2a = 6
Độ dài trục nhỏ là B1B2 = 2b = 4.
Đúng 0
Bình luận (0)
Cho elip (E) có phương trình:
x
2
100
+
y
2
36
1
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
Đọc tiếp
Cho elip (E) có phương trình: x 2 100 + y 2 36 = 1
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.
b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
a) (E):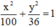 
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
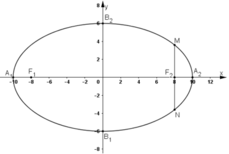
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
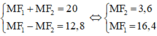
Vậy MN = 2.MF2 = 7,2.
Đúng 0
Bình luận (0)
Xác định độ dài trục lớn, trục nhỏ, tiêu cự, tâm sai, tiêu điểm, đỉnh, đường chuẩn của elip:
\(\left(E\right):4x^2+9y^2-36=0\)
Giúp cần gấp
Ta có: \(\left(E\right):4x^2+9y^2=36\Leftrightarrow\frac{x^2}{9}+\frac{y^2}{4}=1\)
\(a^2=9\Rightarrow a=3\)
\(b^2=4\Rightarrow b=2\)
\(c^2=a^2-b^2=9-4=5\Rightarrow c=\sqrt{5}\)
Tọa độ các đỉnh: \(A_1\left(-3;0\right),A_2\left(3;0,\right),B_1\left(0;-2\right),B_2\left(0;2\right)\)
Tọa độ các tiêu điểm: \(F_1\left(-\sqrt{5};0\right),F_2\left(\sqrt{5};0\right)\)
Độ dài trục lớn \(A_1A_2\div2a=6\)
Độ dài trục nhỏ \(B_1B_2\div2b=4\)
Tiêu cự: \(2c=2\sqrt{5}\)
Tâm sai: \(e=\frac{c}{a}=\frac{\sqrt{5}}{3}\)
Đường chuẩn: \(x=\pm\frac{a^2}{c}=\pm\frac{9}{\sqrt{5}}\)
Đúng 0
Bình luận (2)
Xác định độ dài các trục, tọa độ các tiêu điểm, tọa độ các đỉnh của elip có phương trình sau: 4 x 2 + 9 y 2 = 1
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10 Phương trình nào sau đây là phương trình của elip (E) A.
x
2
25
+
y
2
16
1
B.
x
2
16
+...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10 Phương
trình nào sau đây là phương trình của elip (E)
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 41 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 41 + y 2 16 = 1
Ta có: độ dài trục nhỏ là 8 nên 2b = 8 => b= 4.
Độ dài tiêu cự là 10 nên 2c = 10 => c= 5.
Lại có : a2= b2+ c2= 16+ 25= 41
Vậy phương trình của Elip là: x 2 41 + y 2 16 = 1
Chọn D.
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E). A.
x
2
25
+
y
2
16
1
B.
x
2
16
+
y
2...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E).
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 25 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 9 + y 2 36 = 1
Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a 2 = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: a 2 - b 2 = c 2 ⇒ b 2 = a 2 - c 2 = 5 2 - 3 2 = 16
Vậy phương trình của elip (E) là:
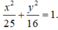
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip ( E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6 . Phương trình nào sau đây là phương trình của elip (E). A.
x
2
25
+
y
2
16
1
B.
x
2
16
+...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho elip ( E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6 . Phương
trình nào sau đây là phương trình của elip (E).
A. x 2 25 + y 2 16 = 1
B. x 2 16 + y 2 25 = 1
C. x 2 36 + y 2 9 = 1
D. x 2 144 + y 2 36 = 0
Ta có: độ dài trục lớn là 10 nên 2a= 10 => a= 5.
Độ dài tiêu cự là 6 nên 2c= 6 => c= 3
Ta có: b2 = a2- c2= 25- 9= 16 => b= 4
Vậy phương trình của Elip là: x 2 25 + y 2 16 = 1
Chọn A.
Đúng 0
Bình luận (0)
Cho Elip
x
2
5
+
y
2
4
1
. Tính tỉ số của tiêu cự với độ dài trục lớn của Elip. A.
5
4
B.
5
5
C. ...
Đọc tiếp
Cho Elip x 2 5 + y 2 4 = 1 . Tính tỉ số của tiêu cự với độ dài trục lớn của Elip.
A. 5 4
B. 5 5
C. 3 5 5
D. 2 5 5
Gọi phương trình chính tắc của Elip có dạng
.
Elip x 2 5 + y 2 4 = 1 có a2= 5; b2= 4 => c2= 5-4= 1 => c= 1
Độ dài trục lớn: 2 a = 2 5 và tiêu cự: 2c= 2
Tỉ số e = 2 c 2 a = 1 5
Chọn B.
Đúng 0
Bình luận (0)
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)? A.
x
2
12
-
y
2
3
1
B.
x
2
12
+
y
2...
Đọc tiếp
Cho elip (E) có độ dài trục lớn gấp hai lần độ dài trục nhỏ và tiêu cự bằng 6. Viết phương trình của (E)?
A. x 2 12 - y 2 3 = 1
B. x 2 12 + y 2 3 = 1
C. x 2 3 + y 2 12 = 1
D. x 2 48 + y 2 12 = 1
