Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x + 2 y + 3 z - 5 = 0 . Đường thẳng Δ vuông góc với (P) cắt d 1 và d 2 có phương trình là:
A. ∆ : x - 1 1 = y + 1 2 = z 3
B. ∆ : x - 2 1 = y - 3 2 = z - 1 3
C. ∆ : x - 3 1 = y - 3 2 = z + 2 3
C. ∆ : x - 1 3 = y + 1 2 = z 1
Trong không gian với hệ trục tọa độ Oxyz, phương trình đường thẳng
d
:
x
-
1
2
y
+
2
1
z
-
1
song song với đường thẳng và cắt hai đường thẳng
d
1
:
x
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, phương trình đường thẳng d : x - 1 2 = y + 2 1 = z - 1 song song với đường thẳng và cắt hai đường thẳng d 1 : x - 1 2 = y + 1 1 = z - 2 - 1 và d 2 : x - 1 2 = y - 2 1 = z - 3 3 là
A. ∆ : x + 1 - 1 = y + 1 1 = z - 2 1
B. ∆ : x - 1 1 = y 1 = z - 1 - 1
C. ∆ : x - 1 1 = y - 2 1 = z - 3 - 1
D. ∆ : x - 1 1 = y - 1 = z - 1 1
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
,
d
2
lần lượt có phương trình
d
1
:
x
-
2
2
y
-
2
1
z
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x - 2 2 = y - 2 1 = z - 3 3 ; d 2 : x - 1 2 = y - 2 - 1 = z - 1 4 . Mặt phẳng cách đều hai đường thẳng có phương trình là
A. 14 x - 4 y - 8 z + 1 = 0
B. 14 x - 4 y - 8 z + 3 = 0
C. 14 x - 4 y - 8 z - 3 = 0
D. 14 x - 4 y - 8 z - 1 = 0
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng
d
1
:
x
−
1
2
y
−
1
z
−
2
và
d
2
:
x...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng d 1 : x − 1 2 = y − 1 = z − 2 và d 2 : x 2 = y − 1 1 = z − 2 1
A. 2 x − 6 y + 4 z − 3 = 0
B. x − 6 y + 8 z − 6 = 0
C. x − 6 y + 4 z − 3 = 0
D. 2 x − 12 y + 8 z − 3 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình
x
−
1
2
y
−
3
z
−
2
0
và mặt phẳng
P
:
x
+
y
0
. Tìm tọa độ điểm M trên d có hoành độ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình x − 1 2 = y − 3 = z − 2 0 và mặt phẳng P : x + y = 0 . Tìm tọa độ điểm M trên d có hoành độ dương sao cho khoảng cách từ M đến (P) bằng 2 .
A. M 3 ; − 3 ; 2
B. M 7 ; − 9 ; 2
C. M 5 ; − 6 ; 2
D. M − 1 ; 3 ; 2
Trong không gian với hệ trục Oxyz, cho ba đường thẳng
d
1
:
x
-
1
2
y
3
z
+
1
-
3
;
d
2
:
x
+
2...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho ba đường thẳng d 1 : x - 1 2 = y 3 = z + 1 - 3 ; d 2 : x + 2 1 = y - 1 - 2 = z 2 ; d 3 : x + 3 - 3 = y - 2 - 4 = z + 5 8 Đường thẳng song song với d 3 , cắt d 1 và d 2 có phương trình là
A. x - 1 - 3 = y - 4 = z + 1 8
B. x - 1 - 3 = y - 4 = z - 1 8
C. x + 1 - 3 = y - 3 - 4 = z 8
D. x - 1 - 3 = y - 3 - 4 = z 8
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình
x
6
+
t
y
-
2
-
5
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình
x
−
1
1
y
+
1
2
z
−
2
−
1
và mặt phẳng
P
:
x
+
2
y...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d có phương trình x − 1 1 = y + 1 2 = z − 2 − 1 và mặt phẳng P : x + 2 y − 2 z + 4 = 0 . Tìm tọa độ điểm M trên d có tung độ dương sao cho khoảng cách từ M đến (P) bằng 2.
A. M 3 ; 3 ; 0
B. M 2 ; 1 ; 1
C. M 0 ; - 3 ; 3
D. M 1 ; - 1 ; 2
Đường cong parabol
y
x
2
6
chia đường elip (E) có độ dài trục lớn và trục bé lần lượt bằng 4 và 2 thành hai phần có tỉ số diện tích bằng (tham khảo hình vẽ bên) A.
S
1
S
2
2
3
5
B.
S...
Đọc tiếp
Đường cong parabol y = x 2 6 chia đường elip (E) có độ dài trục lớn và trục bé lần lượt bằng 4 và 2 thành hai phần có tỉ số diện tích bằng (tham khảo hình vẽ bên)
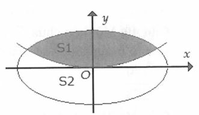
A. S 1 S 2 = 2 3 5
B. S 1 S 2 = 2 π + 3 4 π - 3
C. S 1 S 2 = 4 π + 3 8 π - 3
D. S 1 S 2 = 3 2