tìm các số nguyên x , y thỏa mãn đẳng thức :
\([(x-y)^2+2(xy+y^2-4y)]\)=xy+y2-4y
Những câu hỏi liên quan
Cho các số x,y thỏa mãn đẳng thức 8x2+y2+1/4x2=4.tìm giá trị lớn nhất, nhỉ nhất của P=xy
Tìm các cặp số nguyên x,y thỏa mãn:2(xy-3)=x
2.(xy - 3) = x
=> 2xy - 6 = x
=> 2xy - x = 6
=> x.(2y - 1) = 6
Vậy x và 2y -1 thuộc ước của 6
tới đây dễ rồi bạn nhé :D => bạn tự làm nhé, bye
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên (x,y) thỏa mãn:
(x+y+1)(xy+x+y) = 5+2(x+y)
cho 2 số dương x,y thỏa mãn x+y<=1. tìm GTNN của biểu thức: P=1/(x^2+y^2) + 504/xy
Bài 1:Cho a,b là các số nguyên tố thỏa mãn: (a-1) chia hết cho b và (b3 - 1) chia hết cho a.Chứng minh: a= b2+b+1
Bài 2:Cho x,y là hai số thực thỏa mãn:
x3 + y3 +3x2 + 4x + 3y2 +4y +4=0.Tìm giá trị lớn nhất của biểu thức P=1/x+1/y
1) Vì a, b là số nguyên tố và a - 1 chia hết cho b nên a là số nguyên tố lẻ >=3 và b =2( vì a -1 chẵn)
b3 - 1 = 7 chia hết cho a, nên a =7. Vậy a = b2 + b + 1( 7 = 22 + 2 + 1)
Đúng 0
Bình luận (0)
Cho x, y là các số thực thỏa mãn: \(\sqrt{x-1}-y\sqrt{y}=\sqrt{y-1}-x\sqrt{x}\) . Tìm giá trị nhỏ nhất của biểu thức: \(S=x^2+3xy-2y^2-4y+5\)
Các cậu giúp hộ tớ ạ~
Tìm các số x, y, z thỏa mãn đẳng thức: \((2x-y)^2+(y-2)^2+\sqrt{(x+y+z)^2}\)\(=0\)
Ta có: \(\left(2x-y\right)^2\ge0\); \(\left(y-2\right)^2\ge0\); \(\sqrt{\left(x+y+z\right)^2}=\left|x+y+z\right|\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}2x-y=0\\y-2=0\\x+y+z=0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=?\\y=?\\z=?\end{matrix}\right.\)
Bạn tự giải :D
Đúng 0
Bình luận (0)
Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
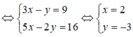
Vậy: T = |x - y| = 5
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên (x;y) thỏa mãn :
x2 + xy - 2013x - 2014y - 2015 = 0