Giúp mình với mình đang cần gấp lắm
cho tam giác ABC nhọn nội tiếp (O), hai đường cao AE và CF cắt nhau tại H
CMR a, tứ giác BEHF nội tiếp
b, tứ giác AFEC nội tiếp
c, OB vuông góc với EF
Chỉ cần làm ý c thôiiii
Những câu hỏi liên quan
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Vẽ 2 đường cao AE và CF cắt nhau tại H.?
a. Chứng minh tứ giác BEHF nội tiếp
b. Chứng minh tứ giác AFEC nội tiếp
c. Chứng minh đường thẳng OB vuông góc với EF
Cho tam giác ABC nội tiếp đường tròn tâm o bán kính 4cm. Vẽ hai đường cao AE và CF cắt nhau tại h a) chứng minh tứ giác BEHF và tứ giác AFEC nội tiếp b tìm dk của o để tam giác ABC vuông tại a
a: Sửa đề: CF là đường cao
góc BEH+góc BFH=180 độ
=>BEHF nội tiếp
góc AFC=góc AEC=90 độ
=>AFEC nội tiếp
b: Để ΔABC vuông tại A thì BC là đường kính của (O)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp (O). vẽ 2 đường cao AE và CF cắt nhau tại H
a, CM tứ giác BEHF nội tiếp
b, CM tứ giác AEC nối tiếp
c, CM OB vuông góc với EF
=(( Ai giúp mk vs ạ !! Mk cần gấp ạk....Câu a và b mk lm đk oy còn câu c.... Thanks m.n nhìu ạ!!!
Cho tam giác ABC nhọn nội tiếp (O), có AB<AC. Vẽ các đường cao BE, CF cắt nhau tại H
a. Chứng minh tứ giác BFEC nội tiếp
b. Chứng minh IE.IB=IF.IC
c. AO vuông góc với EF
(Giúp mình vẽ hình và giải bài với ạ, mình xin cảm ơn)
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: Sửa đề; HE*HB=HF*HC
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HE*HB=HF*HC
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc AO
Đúng 0
Bình luận (0)
giải giúp mình bài này với mình đang cần gấp
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
Giải thích các bước giải:
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH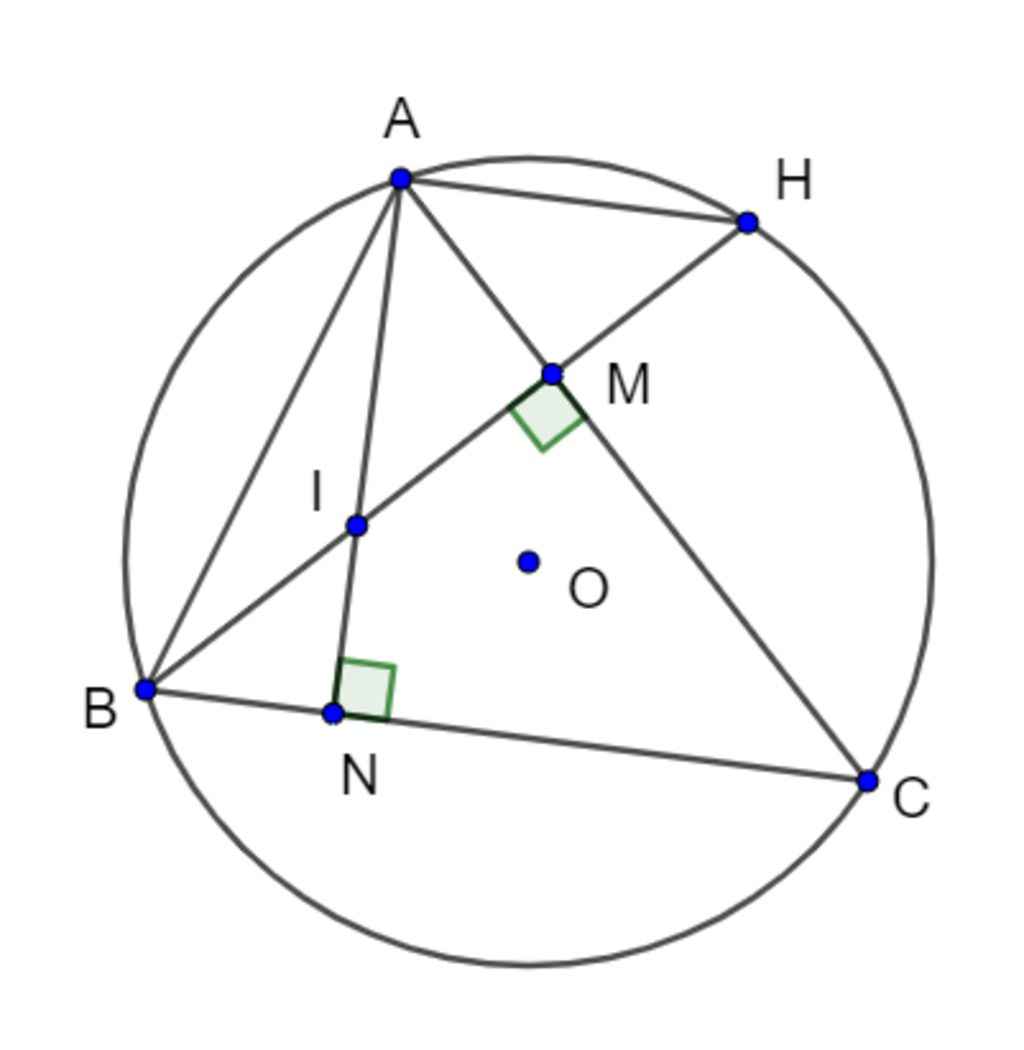
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Vẽ 2 đường cao AE và CF cắt nhau tại H.?
a. Chứng minh tứ giác BEHF nội tiếp
b. Chứng minh tứ giác AFEC nội tiếp
c. Chứng minh đường thẳng OB vuông góc với EF.
a, Xét tứ giác BEHF có: góc BFH + góc BEH = 900 + 900 = 1800
=> Tứ giác BEHF nội tiếp.
b, Xét tứ giác AFEC có :
góc AFC = góc AEC ( = 900) (Hai góc cùng nhìn 1 cạnh dưới 1 góc vuông)
=> Tứ giác AFEC nội tiếp
Đúng 0
Bình luận (0)
Giải hộ bài này vs mn.
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Vẽ 2 đường cao AE và CF cắt nhau tại H.
a.Chứng minh tứ giác BEHF nội tiếp
b.Qua B vẽ tiếp tuyến Bn của (O). Chứng minh Bn //EF.
c.Tia BO cắt đường tròn tại M, HM cắt AC tại K. Chứng minh OK vuông góc với AC
cho tam giác ABC nhọn đường cao BM,CN cắt nhau tại H. CMR:
a, tứ giác AMHN nội tiếp
b, BCMN nội tiếp
c, AH cắt BC tại I. CMR: IA là tia phân giác của góc MIN.
mình cần giải gấp câu (c) còn câu a và b mình giải được rồi. Giúp mình với
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Hai đường cao BE và CF cắt nhau tại H. Tia AO cắt đường tròn tại D . Chứng minh
a) tứ giác AEHF nội tiếp đường tròn
B) tứ giác BHCD là hình bình hành
c) tứ giác BFEc nội tiếp được đường tròn
d) Tam giác AEF ~ tam giác ABC, suy ra AE.AC = AF.AB
a) Xét tứ giác AEHF có
\(\widehat{HFA}\) và \(\widehat{HEA}\) là hai góc đối
\(\widehat{HFA}+\widehat{HEA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời