Cho ĐTHS y=ax^2 có đồ thị là (p) và ĐThẳng y=x+3. a) vẽ ĐTHS (p) b) XĐ toạ độ giao điểm của (p) và (d)

Những câu hỏi liên quan
cho 2 hàm số : y=3x và y=-x+3
a. vẽ đths trên cùng 1 mặt phẳng toạ độ
b. xác định hs y=ax+b (a khác 0) bt rằng đths đó cắt đt y=-x+2 tại 1 điểm trên trục tung và đi qua điêm A(1;3)
c. tìm điểm thuộc đt y=-x+2 có hoành độ gấp 3 tung độ
b: Vì (d) cắt y=-x+2 tại trục tung nên
a<>-1 và b=2
=>y=ax+2
Thay x=1 và y=3 vào y=ax+2, ta được:
a+2=3
=>a=1
c: Thay x=3y vào y=-x+2, ta được;
y=-3y+2
=>4y=2
=>y=1/2
=>B(3/2;1/2)
Đúng 0
Bình luận (0)
Bài tập 1 Cho (P) yx^2 và đthg (D)y-x+2 a,Tìm tọa độ giao điểm của (P) và (D)b, Viết pt đthg (D)biết (D)song song với (D) và cắt (P)tại điểm có hoành độ -1Bài tập 2 Cho hs y-3x+b .Hãy xác định b nếu :a,Đths cắt trục tung tại 3 b, Đths cắt đths y6x+5 tại 1 điểm nằm trên trục tung c, Đồ thị tiếp xúc hs tiếp xúc parabol yx^2MÌNH CẦN GẤP NHA ! CẢM ƠN Ạ!
Đọc tiếp
Bài tập 1 Cho (P) y=x^2 và đthg (D)y=-x+2
a,Tìm tọa độ giao điểm của (P) và (D)
b, Viết pt đthg (D)biết (D)song song với (D) và cắt (P)tại điểm có hoành độ -1
Bài tập 2 Cho hs y=-3x+b .Hãy xác định b nếu :
a,Đths cắt trục tung tại 3
b, Đths cắt đths y=6x+5 tại 1 điểm nằm trên trục tung
c, Đồ thị tiếp xúc hs tiếp xúc parabol y=x^2
MÌNH CẦN GẤP NHA ! CẢM ƠN Ạ!
Cho hàm số y=2/3 x2 có đồ thị P và y= x + 5/3 có đồ thị D a. Vẽ P và D trên cùng một hệ trục toạ độ vuông góc b. Xác định toạ độ các giao điểm của P và D c. Gọi A là điểm thuộcP và B là điểm thuộc D sao cho { x A = x B 11 y A = 8 y B xác định toạ độ của A và B
Cho 2 hàm số y= 2x-3 (d1) và y= \(\dfrac{1}{2}\)x+3 (d2)
a, Vẽ đths y= 2x-3 trên hệ toạ trục Oxy
b, Gọi giao điểm của 2 đường thẳng (d1) và (d2) là M. Tìm toạ độ điểm M bằng phương pháp đại số
GIÚP MÌNH VỚI
a: 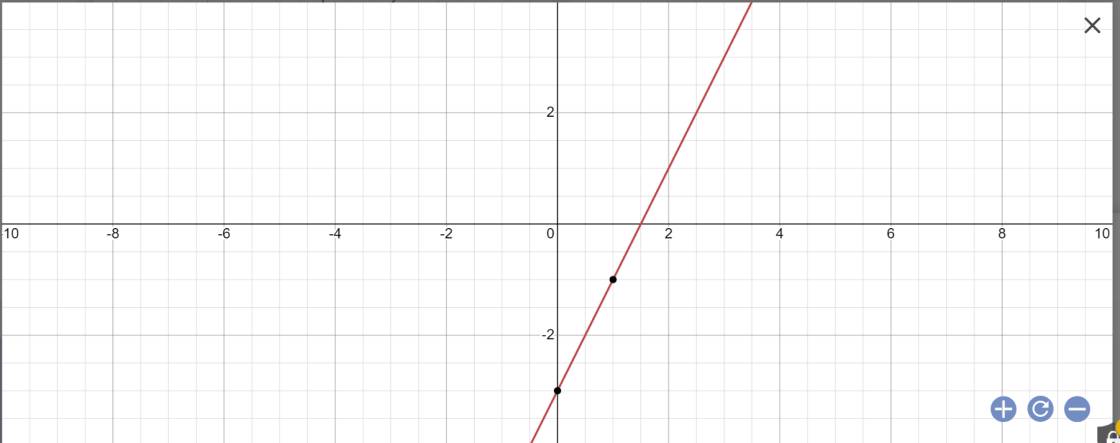
b: Phương trình hoành độ giao điểm là:
\(2x-3=\dfrac{1}{2}x+3\)
=>\(2x-\dfrac{1}{2}x=3+3=6\)
=>\(\dfrac{3}{2}x=6\)
=>\(x=6:\dfrac{3}{2}=4\)
Thay x=4 vào y=2x-3, ta được:
\(y=2\cdot4-3=5\)
Vậy: M(4;5)
Đúng 3
Bình luận (0)
Câu 1 : Cho đồ thị (C) của hàm số y = x2 - 4x + m và đường thẳng (d) y = -x +1
a) Lập bảng biến thiên và vẽ đồ thị hàm số (C) khi m =3 . Xác định toạ độ giao điểm của đths vừa vẽ với đường thẳng (d) bằng phép tính . b) Tìm m đê (d) cắt (C) tại hai điểm phâm biệt A,B . Xác định toạ độ trung điểm của đoạn thẳng AB
a: Khi m=3 thì (C): y=x^2-4x+3
PTHĐGĐ là:
x^2-4x+3=-x+1
=>x^2-4x+3+x-1=0
=>x^2-3x+2=0
=>x=1 hoặc x=2
=>y=-1+1=0 và y=-2+1=-1
b: PTHĐGĐ là:
\(x^2-4x+m=-x+1\)
=>x^2-4x+m+x-1=0
=>x^2-3x+m-1=0
Δ=(-3)^2-4(m-1)
=9-4m+4=-4m+13
Để (C) cắt (d) tại hai điểm phân biệt thì -4m+13>0
=>-4m>-13
=>m<13/4
Đúng 0
Bình luận (0)
a) Vẽ đồ thị của hàm số y=2x-5 (d1)
b) Xác định các hệ số a và b của hàm số y=ax=b (d2) , biết rằng đths d2 song song với đths d1 và cắt trục hoành tại điểm có hoành độ bằng 5
cho hàm số y=f(x)= -x2
a) Vẽ đồ thị hàm số
b) tính f(-1) , f(1/2)
c)điểm E(1;-1) , F(-2;4) có thuộc đths không ?
d)tìm tung độ của điểm thuộc đths trên có hoành độ -3
e) tìm hoành độ của điểm thuộc đths trên có tung độ -3
giúp em với ạ!!!
b: f(-1)=-1
f(1/2)=-1/4
c: \(f\left(1\right)=-1^2=-1=y_E\)
Do đó: E thuộc đồ thị
\(f\left(-2\right)=-\left(-2\right)^2=-4< >y_F\)
Do đó: F không thuộc đồ thị
d: Thay x=-3 vào f(x), ta được:
\(f\left(-3\right)=-\left(-3\right)^2=-9\)
Đúng 1
Bình luận (0)
Cho hàm số y=3/2 x^2 (P) và y=x+1/2 (d) a) vẽ đồ thị (P) và (d) trên cùng một mặt phẳng toạ độ. b) tìm toạ độ giao điểm của (P) và (d). c) viết phương trình đường thẳng cắt (P) tại 2 điểm có hoành độ là -4 và 2.
a)Tự vẽ
b) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
\(\Leftrightarrow3x^2-2x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\Rightarrow y=\dfrac{3}{2}.\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{6}\\x=1\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy gđ của (d) và (P) là \(\left(-\dfrac{1}{3};\dfrac{1}{6}\right),\left(1;\dfrac{3}{2}\right)\)
c) Gọi đt cần tìm có dạng (d') \(y=ax+b\) (a2+b2>0)
Gọi A(-4;y1) và B(2;y2) là hai giao điểm của (P) và (d')
\(A;B\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}y_1=24\\y_2=6\end{matrix}\right.\)
\(\Rightarrow A\left(-4;24\right),B\left(2;6\right)\) \(\in\left(d'\right)\)
\(\Rightarrow\left\{{}\begin{matrix}24=-4a+b\\6=2a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=12\end{matrix}\right.\) (thỏa)
Vậy (d'): y=-3x+12
Đúng 1
Bình luận (0)
Cho hàm số y=1/2 x^2 có đồ thị là (P) a) Vẽ đồ thị (P) của hàm số trên b) Tìm toạ độ giao điểm của (P) và đường thẳng (d) : y = x + 4
b: PTHĐGĐ là:
1/2x^2-x-4=0
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
=>y=8 hoặc y=2
a: 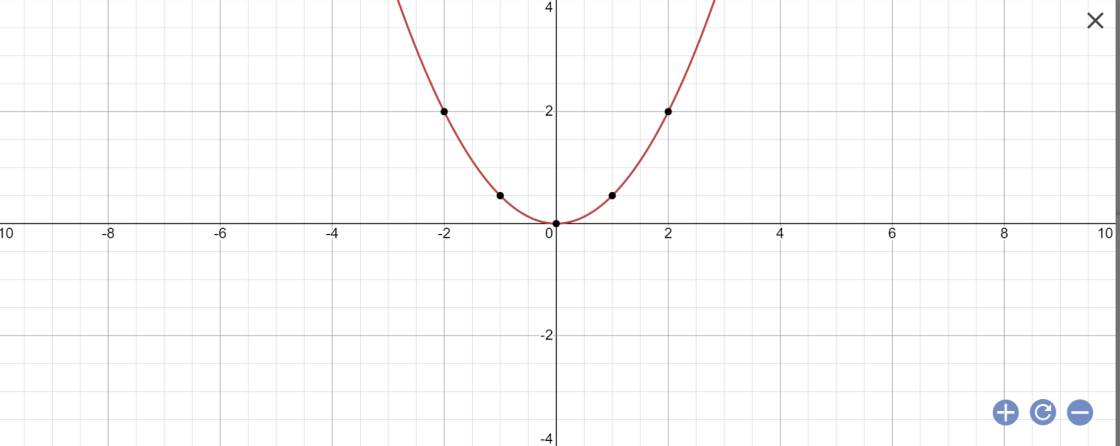
Đúng 0
Bình luận (0)


















