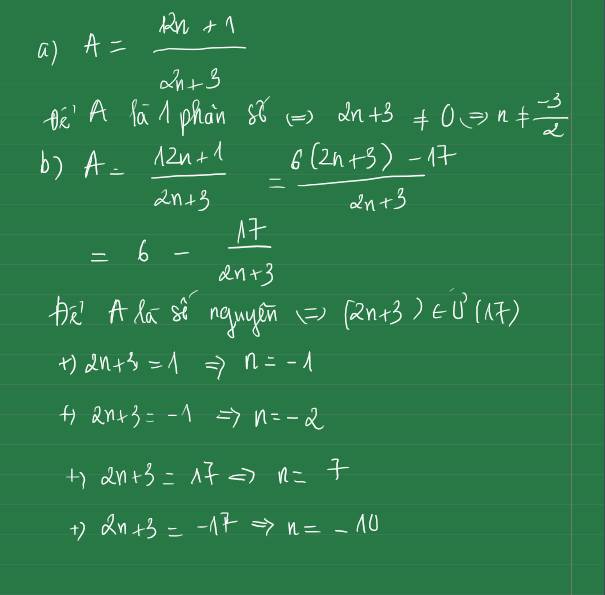\(\text{Tìm số nguyên n để phân số A=}\dfrac{12n-1}{4n-3}\text{có giá trị nhỏ nhất}\)

Những câu hỏi liên quan
tìm số nguyên n để phân số A=12n-1/4n+4 có giá trị nhỏ nhất
cho phân số: A=12n-2/4n+1
tìm số nguyên n để A có giá trị nguyên
cho A= 12n/3n+3. tìm giá trị của n để:a.A là một phân số. b.A là một số nguyên c. với giá trị nào của stn n thì a có giá trị nhỏ nhất và giá trị nhỏ nhất đó bằng bao hiêu
a: Để A là phân số thì 3n+3<>0
hay n<>-1
b: Để A là số nguyên thì \(4n⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)
Đúng 1
Bình luận (0)
Cho A = \(\dfrac{12n}{3n+3}\)
a) A là 1 phân số
b) A là số nguyên
c) Với giá trị nào của số tự nhiên n thì A có giá trị nhỏ nhất và giá trị nhỏ nhất đó bằng bao nhiêu
a: Để A là phân số thì 3n+3<>0
=>n<>-1
b: \(A=\dfrac{12n}{3\left(n+1\right)}=\dfrac{4n}{n+1}\)
Để A là số nguyên thì 4n+4-4 chia hết cho n+1
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)
Đúng 0
Bình luận (0)
Câu 1:Cho A=\(\dfrac{12n+1}{2n+3}\\\).Tìm giá trị của n để:
a)A là 1 phân số.
b)A là 1 số nguyên.
a) Để A là một phân số thì mẫu của \(A\ne0\) hay \(2n+3\ne0\)
\(\Leftrightarrow n\ne\dfrac{-3}{2}\)
b) Ta có : \(A=\dfrac{12n+1}{2n+3}\)
\(\Rightarrow A=\dfrac{12n+18-17}{2n+3}=\dfrac{12n+18}{2n+3}-\dfrac{17}{2n+3}\)
\(\Rightarrow A=\dfrac{6\left(2n+3\right)}{2n+3}-\dfrac{17}{2n+3}=6-\dfrac{17}{2n+3}\)
Để \(A\in Z\Leftrightarrow\dfrac{17}{2n+3}\in Z\)
\(\Leftrightarrow2n+3\in U\left(17\right)\)
mà \(U\left(17\right)=\left(1;-1;17;-17\right)\)
\(\Rightarrow n\in\left(-1;-2;7;-10\right)\)
Vậy \(A\in Z\Leftrightarrow n\in\left(-1;-2;7;-10\right)\)
Đúng 2
Bình luận (0)
A= \(\dfrac{12n}{3n+3}\)
Tìm giá trị của n đề:
a) A là một phân số
b) A là một số nguyên
c) Với giá trị nào của số tự nhiên n thì A có giá trị nhỏ nhất và giá trị nhỏ nhất đó bằng bao nhiêu?
Giúp mình với mình đang cần gấp!!!
a: A là phân số khi 3n+3<>0
=>n<>-1
b: \(A=\dfrac{12}{3\left(n+1\right)}=\dfrac{4}{n+1}\)
Để A nguyên thì \(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)
Đúng 1
Bình luận (0)
Tìm số nguyên n để A=\(\frac{4n+1}{2n+3}\)
a) A là phân số khi nào?
b)A có giá trị là 1 số nguyên?
c)A có giá trị lớn nhất?
d) A có giá trị nhỏ nhất?
Cho A = \(\frac{4n+1}{2n+3}\). Tìm n thuộc Z để:
a) A là phân số.
b) A có giá trị là một số nguyên.
c) A có giá giá trị lớn nhất. A có giá trị nhỏ nhất
Cho A = 4n+1 / 2n+3 (n là số nguyên).
a) Tìm n để A nguyên
b) Tìm n để A có giá trị lớn nhất, nhỏ nhất
\(\frac{4n+1}{2n+3}=\frac{4n+6-5}{2n+3}=\frac{2\left(2n+3\right)-5}{2n+3}=2-\frac{5}{2n+3}\)
Để \(2-\frac{5}{2n+3}\) là số nguyên <=> \(\frac{5}{2n+3}\) là số nguyên
=> 2n + 3 thuộc Ư(5) = { - 5; - 1; 1; 5 }
=> 2n + 3 = { - 5; - 1; 1; 5 }
=> n = { - 4; - 2; - 1 ; 1 }
Đúng 0
Bình luận (0)
a) Ta có:
\(\frac{4n+1}{2n+3}\inℤ\)
\(\Rightarrow\frac{4n-2+3}{2n+3}\inℤ\)
\(\Rightarrow\frac{2n+2n+3-2}{2n+3}\inℤ\)
\(\Rightarrow\frac{2n+3}{2n+3}+\frac{2n-2}{2n+3}\inℤ\)
\(\Rightarrow1+\frac{2n-2}{2n+3}\inℤ\Leftrightarrow\frac{2n-2}{2n+3}\inℤ\)
\(\Rightarrow\frac{2n+3-5}{2n+3}\inℤ\)
\(\Rightarrow1+\frac{-5}{2n+3}\inℤ\Leftrightarrow\frac{-5}{2n+3}\inℤ\)
\(\Rightarrow\left(2n+3\right)\in B\left(-5\right)=\left\{1;-1;5;-5\right\}\)
\(\Rightarrow\left(2n+3\right)=\left\{1;-1;5;-5\right\}\)
\(\Rightarrow2n=\left\{-2;-4;2;-8\right\}\)
\(\Rightarrow n=\left\{-1;-2;1;-4\right\}\)
Xem thêm câu trả lời