Cho điểm O nằm ngoài đường thẳng a. Trên đường thẳng a xác định 10 điểm A1;A2;A3;A4;A5;A6;A7;A8;A9;A10. Qua 3 điểm không thẳng hàng vẽ được 1 tam giác. Có bao nhiêu tam giác trên hình vẽ.
cho các điểm A1,A2,A3 nằm trên đường thẳng a: các điểm B1,B2,B3,B4 nằm trên dường thẳng b.Hãy xác định số tam giác có ba đỉnh là ba trong số 7 điểm nói trên
Số tam giác có được là:
\(C^2_3\cdot C^1_4+C^1_3\cdot C^2_4=30\)
1 tam giác có 3 đỉnh ko thẳng hàng.
Theo NL Đi-rích-lê, có 3 điểm, 2 đường thẳng => Có 1 đường thẳng chứa 2 điểm, đường thẳng kia chứa điểm còn lại
Ta chia trường hợp:
*TH1: 2 điểm trên đường thẳng a, 1 điểm trên đường thẳng b
+) Điểm 1 trên a có 3 cách chọn
Điểm 2 trên a có 2 cách chọn
+) Điểm 1 trên b có 1 cách chọn
=> Tạo được 3.2.1 = 6 (tam giác)
*TH2: 1 điểm trên a, 2 điểm trên b
+) Điểm 1 trên a có 1 cách chọn
+) Điểm 1 trên b có 4 cách chọn
Điểm 2 trên b có 3 cách chọn
=> Tạo được 1.3.4 = 12 (tam giác)
Vậy tạo được tất cả 6+12=18 tam giác từ 7 điểm trên.
cho 1o điểm nằm trên đường thẳng a và điểm O nằm ngoài đường thẳng a . nối điểm O với 10 điểm đó. Hỏi trên hình vẽ có bao nhiêu tam giác
Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)
Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)
Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)
Ai ngang qua nhớ k
Cho 2 đường tròn ngoài nhau ( O ; R ) và ( O' ; R' ) . A nằm trên đường tròn ( O ) , B nằm trên đường tròn ( O' ) . Xác định vị trí của các điểm A , B để đoạn thẳng AB có độ dài lớn nhất . nhỏ nhất .
Theo quy tắc 4 điểm thì \(\hept{\begin{cases}OA+AB+O'B\ge OO'\\OA+OO'+O'B\ge AB\end{cases}}\Leftrightarrow\hept{\begin{cases}AB\ge OO'-\left(R+R'\right)\left(const\right)\\AB\le OO'+\left(R+R'\right)\left(const\right)\end{cases}}\)
=> AB nhỏ nhất khi A, B nằm giữa OO' ; A, B lớn nhất khi OO' nằm giữa AB
Cho điểm A nằm ngoài đường thẳng d trên đường d lần lượt lấy các điểm A1; A2; A3;................; A8. Hỏi trên hình vẽ có bao nhiêu đường thẳng ( không tính các đường thẳng trùng nhau )
Cho điểm A nằm ngoài đường thẳng a. Trên đườn thẳng a lấy các điểm A1, A2, A3,.....,A100. Hỏi với các điển trong đường thẳng a, vẽ được bao nhiêu tam giác ?
Các bạn trả lời kĩ hộ mình, mình cần gấp
Ta có 100 điểm lần lượt là A1, A2,...,A100.
-> Có 100 đoạn thẳng nối với A đến các điểm đó.
Mỗi đoạn thẳng kết hợp với 99 đoạn thẳng còn lại và các đoạn thẳng tương ứng trên đoạn thẳng đó để tạo thành 99 tam giác.
Do đó 100 đoạn thẳng tạo thành : 99 . 100. Vì mỗi tam giác lặp lại 2 lần
=> Nên số tam giác được tao thành là:
(99 . 100) : 2 = 4950 tam giác
Vậy số tam giác được tạo thành là 4950 tam giác
Cho n điểm A1; A2; . . . ; An theo thứ tự trên đường thẳng xy và điểm M nằm ngoài đường thẳng xy. Nối M với n điểm đó ta đếm được 55 tam giác. Vậy giá trị của n là:
A. 10 B. 11 C. 12 D. 15
Cho n điểm A1; A2; . . . ; An theo thứ tự trên đường thẳng xy và điểm M nằm ngoài đường thẳng xy. Nối M với n điểm đó ta đếm được 55 tam giác. Vậy giá trị của n là:
A. 10 B. 11C. 12 D. 15
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
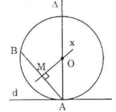
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.
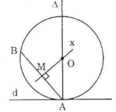
Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.
Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.
Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.
Cho A là một điểm bất kì nằm ngoài đường thẳng d. Xác định khoảng cách từ A đến đường thẳng d
Chỉ cần vẽ đường cao kẻ từ A xuống d