sử dụng công thức nghiệm để giải phương trình sau 4x² + 4x + 3 = 0

Những câu hỏi liên quan
Giải phương trình sau sử dụng công thức nghiệm: 4x^2 - 12x + 9 = 0
Xem chi tiết
Ta có: \(\Delta=b^2-4ac=\left(-12\right)^2-4.4.9=144-144=0\)
Vì \(\Delta=0\)nên pt có 2 nghiệm kép
\(x_1=x_2=\frac{-b}{2a}=\frac{12}{2.4}=\frac{3}{2}\)
Vậy ......
Áp dụng công thức nghiệm để giải các phương trình: 4x2 – 4x + 1 = 0
4x2 – 4x + 1 = 0;
a = 4; b = -4; c = 1
Δ = b2 - 4ac = (-4)2 - 4.4.1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
Đúng 0
Bình luận (0)
Áp dụng công thức nghiệm để giải các phương trình:
a
)
5
x
2
−
x
+
2
0
b
)
4
x
2
−
4
x...
Đọc tiếp
Áp dụng công thức nghiệm để giải các phương trình:
a ) 5 x 2 − x + 2 = 0 b ) 4 x 2 − 4 x + 1 = 0 c ) − 3 x 2 + x + 5 = 0
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
Đúng 0
Bình luận (0)
Bài 1. Sử dụng công thức nghiệm của phương trình bậc hai giải các phương trình sau:
a. 6x2 + x – 5 = 0
b. 3x2 + 4x + 2 = 0
c. x2 – 8x + 16 = 0
giúp mik vs mik làm hôm nay nộp r
a,\(6x^2+x-5=0\)
\(\Delta=b^2-4ac=1^2-4.6.\left(-5\right)=1+120=121\)
Vì \(\Delta>0\)nên pt có 2 nghiệm phân biệt
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1-\sqrt{121}}{2.6}=\frac{-1-11}{12}=\frac{-12}{12}=-1\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1+\sqrt{121}}{2.6}=\frac{-1+11}{12}=\frac{10}{12}=\frac{5}{6}\)
Vậy \(S=\left\{-1;\frac{5}{6}\right\}\)
b, \(3x^2+4x+2=0\)
\(\Delta=b^2-4ac=4^2-4.3.2=16-24=-8\)
Vì \(\Delta< 0\)nên pt vô nghiệm
c, \(x^2-8x+16=0\)
\(\Delta=b^2-4ac=\left(-8\right)^2-4.1.16=64-64=0\)
Vì \(\Delta=0\)nên pt có nghiệm kép
\(x_1=x_2=\frac{-b}{2a}=\frac{-b'}{a}=\frac{8}{4}=\frac{4}{2}=2\)
a) \(6x^2+x-5=0\)
Ta có : \(\Delta=1+4.6.5=121>0\)
\(\Rightarrow\sqrt{\Delta}=11\)
Phương trình có hai nghiệm :
\(x_1=\frac{-1+11}{2.6}=\frac{5}{6}\)
\(x_2=\frac{-1-11}{2.6}=-1\)
b) \(3x^2+4x+2=0\)
Ta có : \(\Delta=4^2-4.3.2=-8< 0\)
Vậy phương trình vô nghiệm
c) \(x^2-8x+16=0\)
Ta có : \(\Delta=\left(-8\right)^2-4.1.16=0\)
Phương trình có nghiệm kép :
\(x_1=x_2=\frac{8}{2}=-4\)
Dùng công thức nghiệm,công thức nghiệm thu gọn giải các phương trình sau:
a.\(x^2-4x-21=0\)
b.\(4x^2+28x+49=0\)
c.\(6y^2-5\sqrt{2}y+2=0\)
d.\(y^2-\left(1+\sqrt{3}\right)y+\sqrt{3}=0\)
e.\(x^2+3x-10=0\)
a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
Đúng 1
Bình luận (1)
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
4x2 + 4x + 1 = 0
Phương trình bậc hai 4x2 + 4x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ’ = (b’)2 – ac = 22 – 4.1 = 0
Phương trình có nghiệm kép là:
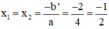
Đúng 0
Bình luận (0)
Tìm m để các phương trình sau (dùng công thức nghiệm thu gọn)
a.\(x^2+2\left(m-2\right)x+m^2-3=0\) có nghiệm
b.\(\left(2m-1\right)x-4mx+2m+3=0\) có nghiệm kép
c.\(4x^2-2\left(2m-1\right)x+m^2=0\) vô nghiệm
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4
Đúng 0
Bình luận (0)
Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn: -7 x 2 + 4x = 3
Phương trình -7 x 2 +4x=3 ⇔ 7x2 -4x+3 = 0 có hệ số a=7, b’=-2 , c=3
Ta có: ∆ ’ = b ' 2 – ac = - 2 2 -7.3 = 4- 21= -17 < 0
Vậy phương trình vô nghiệm
Đúng 0
Bình luận (0)














