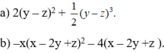a)

$x^4-2x^3+2x-1=(x^4-2x^3+x^2)-(x^2-2x+1)$

$=(x^2-x)^2-(x-1)^2$

$=x^2(x-1)^2-(x-1)^2=(x-1)^2(x^2-1)=(x-1)^2(x-1)(x+1)$

$=(x-1)^3(x+1)$

b)

$a^6-a^4+2a^3+2a^2$

$=a^4(a^2-1)+2a^2(a+1)$

$=a^4(a-1)(a+1)+2a^2(a+1)$

$=(a+1)[a^4(a-1)+2a^2]$

$=a^2(a+1)[a^2(a-1)+2]$

$=a^2(a+1)(a^3-a^2+2)=a^2(a+1)[a^2(a+1)-2(a^2-1)]$

$=a^2(a+1)[a^2(a+1)-2(a-1)(a+1)]$

$=a^2(a+1)(a+1)(a^2-2a+2)=a^2(a+1)^2(a^2-2a+2)$

c)

$x^4+x^3+2x^2+x+1$

$=(x^4+2x^2+1)+(x^3+x)$

$=(x^2+1)^2+x(x^2+1)=(x^2+1)(x^2+1+x)$

d)

$x^4+2x^3+2x^2+2x+1$

$=(x^4+2x^3+x^2)+(x^2+2x+1)$

$=(x^2+x)^2+(x+1)^2=x^2(x+1)^2+(x+1)^2$

$=(x+1)^2(x^2+1)$

e)

$x^2y+xy^2+x^2z+y^2z+2xyz$

$=xy(x+y)+z(x^2+y^2)+2xyz$

$=xy(x+y)+z(x^2+y^2+2xy)$

$=xy(x+y)+z(x+y)^2=(x+y)(xy+zx+zy)$

f)

$x^5+x^4+x^3+x^2+x+1$

$=(x^5+x^4)+(x^3+x^2)+(x+1)=x^4(x+1)+x^2(x+1)+(x+1)$

$=(x+1)(x^4+x^2+1)$

$=(x+1)[(x^4+2x^2+1)-x^2]$

$=(x+1)[(x^2+1)^2-x^2]=(x+1)(x^2+1-x)(x^2+1+x)$

a: =-1/5x^5y^2

b: =-9/7xy^3

c: =7/12xy^2z

d: =2x^4

e: =3/4x^5y

f: =11x^2y^5+x^6

help me ai nhanh nhất mik tích cho

a) Ta có: \(\left(\dfrac{3}{4}\right)^{2021}>\left(\dfrac{3}{4}\right)^1=\dfrac{3}{4}\)

\(\Leftrightarrow\left(\dfrac{3}{4}\right)^{2021}+1>\dfrac{3}{4}+1\)

Tìm x,y 

Ta có: \(\frac{x}{3}=\frac{y}{4}\)

\(\Rightarrow y=\frac{4x}{3}\)  ( 1 )

Ta có: \(\frac{x}{3}=\frac{z}{5}\)

\(\Rightarrow z=\frac{5x}{3}\)   ( 2 ) 

Theo đề bài: 2x + y = 2z  ( 3 ) 

Thay ( 1 ), ( 2 ) vào ( 3 ) ta được một phương trình mới: 

\(2x+\frac{4x}{3}=2.\left(\frac{5x}{3}\right)\)

\(\Leftrightarrow\frac{6x+4x}{3}=\frac{10x}{3}\)

\(\Leftrightarrow6x+4x=10x\)

\(\Leftrightarrow10x=10x\)

\(\Leftrightarrow x=x\)  ( Vô số nghiệm ) 

\(\Rightarrow x\in R\)    ( R là số thực, có nghĩa là tất cả các số trong vũ trụ này nha ) 

Ta có: \(x\in R\) 

\(\Rightarrow y\in R\)

Vậy \(x,y\in R\)

a)\(\left|2x-3y\right|+\left|2y-4z\right|=0\)

\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\forall x;y\\\left|2y-4z\right|\ge0\forall y;z\end{matrix}\right.\) \(\Rightarrow\left|2x-3y\right|+\left|2y-4z\right|\ge0\)

Dấu "=" xảy ra khi:

\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|2y-4z\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=3y\\2y=4z\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{2}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{6}=\dfrac{y}{4}\\\dfrac{y}{4}=\dfrac{z}{2}\end{matrix}\right.\)

\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{2}=\dfrac{x+y+z}{6+4+2}=\dfrac{7}{12}\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{12}.6=\dfrac{7}{2}\\y=\dfrac{7}{12}.4=\dfrac{7}{3}\\z=\dfrac{7}{12}.2=\dfrac{7}{6}\end{matrix}\right.\)

b)\(\left|x-2\right|+\left|x-3\right|+\left|x-4\right|=0\)

\(\left\{{}\begin{matrix}\left|x-2\right|\ge0\\\left|x-3\right|\ge0\\\left|x-4\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|x-2\right|+\left|x-3\right|+\left|x-4\right|\ge0\)

Dấu "=" xảy ra khi:

\(\left\{{}\begin{matrix}\left|x-2\right|=0\\\left|x-3\right|=0\\\left|x-4\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=3\\x=4\end{matrix}\right.\)

Vì \(2\ne3\ne4\) nên \(x\in\varnothing\)

c)

\(\left|x+1\right|+\left|x+2\right|+...+\left|x+8\right|+\left|x+9\right|\)

Với mọi \(x\ge0\) ta có:

\(\left\{{}\begin{matrix}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\\\left|x+8\right|=x+8\\\left|x+9\right|=x+9\end{matrix}\right.\)\(\Leftrightarrow x+1+x+2+...+x+8+x+9=x-1\)

\(\Leftrightarrow9x+90=x-1\)

\(\Leftrightarrow9x=x-89\)

\(\Leftrightarrow-8x=89\)

\(\Leftrightarrow x=\dfrac{89}{-8}\left(KTM\right)\)

Với mọi \(x< 0\) ta có:

\(\left\{{}\begin{matrix}x+1=-x-1\\x+2=-x-2\\x+8=-x-8\\x+9=-x-9\end{matrix}\right.\) \(\Leftrightarrow\left(-x-1\right)+\left(-x-2\right)+...+\left(-x-8\right)+\left(-x-9\right)=x-1\)

\(\Leftrightarrow-9x-90=x-1\)

\(\Leftrightarrow-9x=x+89\)

\(\Leftrightarrow-10x=89\)

\(\Leftrightarrow x=\dfrac{89}{-10}\left(TM\right)\)

d)\(\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|=0\)

\(\left\{{}\begin{matrix}\left|2x-3y\right|\ge0\\ \left|5y-2z\right|\ge0\\ \left|2z-6\right|\ge0\end{matrix}\right.\) \(\Leftrightarrow\left|2x-3y\right|+\left|5y-2z\right|+\left|2z-6\right|\ge0\)

Dấu "=" xảy ra khi:

\(\left\{{}\begin{matrix}\left|2x-3y\right|=0\\\left|5y-2z\right|=0\\\left|2z-6\right|=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}z=3\\y=\dfrac{6}{5}\\x=\dfrac{9}{5}\end{matrix}\right.\)