tìm a, b, c, d biết :
x4 + ax3 + bx2 -8x + 4= ( x2 + cx + d)
Những câu hỏi liên quan
Cho đa thức: f(x)=x4+ax3+bx2+cx+df(x)=x4+ax3+bx2+cx+d ( với a, b, c, d là các số thực). Biết f(1)=10; f(2)=20; f(3)=30. Tính giá trị của biểu thức: A=f(9)+f(-5
)
Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)
Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)
Chúc bạn hok tốt <3
Đúng 3
Bình luận (0)
Cho hàm số y f(x ) ax3+ bx2+ cx+ d có bảng biến thiên như sau: Khi đó |f(x)| m có 4 nghiệm phân biệt
x
1
x
2
x
3
1
2
x
4
khi và chỉ khi A. ½ m 1 B. 0 m C. m 1 D. m 1/2
Đọc tiếp
Cho hàm số y= f(x )= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
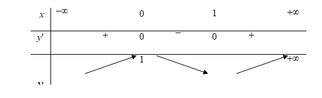
Khi đó |f(x)| = m có 4 nghiệm phân biệt x 1 < x 2 < x 3 < 1 2 < x 4 khi và chỉ khi
A. ½< m< 1
B. 0< m
C. m> 1
D. m< 1/2
Ta có f ( 0 ) = 0 f ( 1 ) = 0 f ' ( 0 ) = 0 f ' ( 1 ) = 0
↔ a = 2 b = - 3 c = 0 d = 1
, suy ra hàm số đã cho là : y= 2x3-3x2+ 1.
Ta thấy: f(x) = 0 ↔ x = 0 hoặc x = -1/2
Bảng biến thiên của hàm số y = |f(x)| như sau:
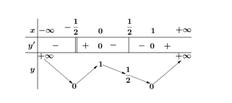
Dựa vào bảng biến thiên suy ra phương trình |f(x)| = m có bốn nghiệm phân biệt x1< x2< x3< ½< x4 khi và chỉ khi ½< m< 1.
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số bậc ba
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
g
(...
Đọc tiếp
Cho hàm số bậc ba f ( x ) = a x 3 + b x 2 + c x + d có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số g ( x ) = ( x 2 - 3 x + 2 ) 2 x + 1 ( x 4 - 5 x 2 + 4 ) . f ( x ) có bao nhiêu đường tiệm cận đứng?
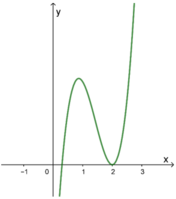
A. 4
B. 3
C. 2
D. 6
\
Cho hàm số
y
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có bảng biến thiên như sau Khi đó
f
x
m
có bốn nghiệm phân biệt
x
1
x
2
x...
Đọc tiếp
Cho hàm số y = f ( x ) = ax 3 + bx 2 + cx + d có bảng biến thiên như sau
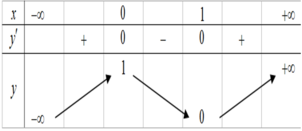
Khi đó f x = m có bốn nghiệm phân biệt x 1 < x 2 < x 3 < 1 / 2 < x 4 khi và chỉ khi
A. 
.
B. 
.
C. 
.
D. 
.
Đáp án B
Ta có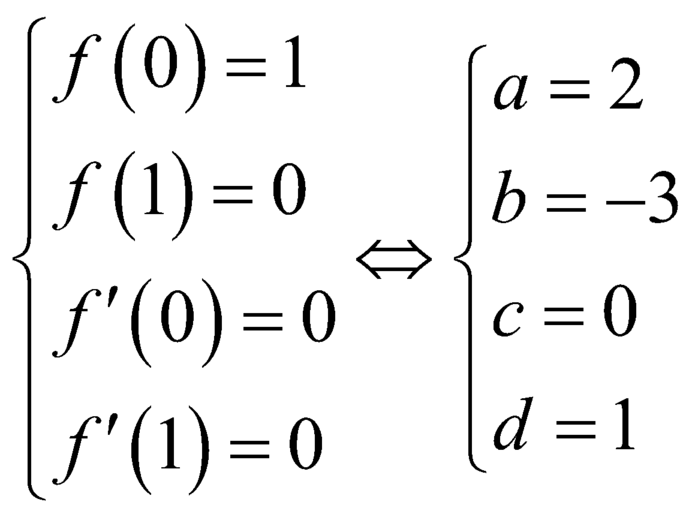 
suy ra 
.
Ta có: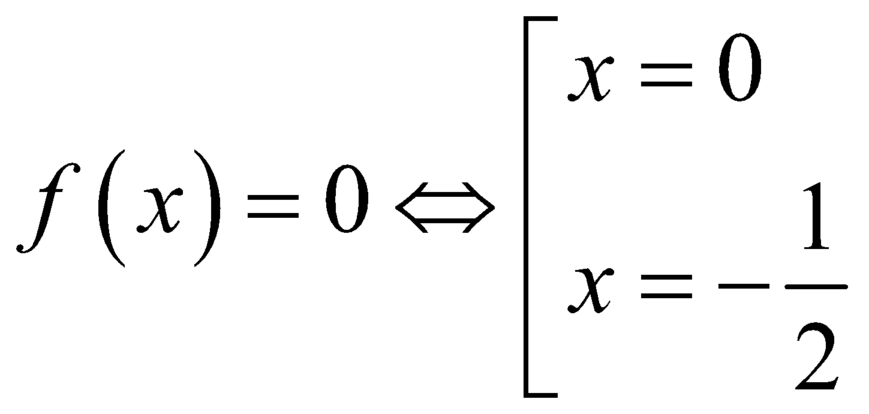 
.
Bảng biến thiên của hàm số 
như sau:
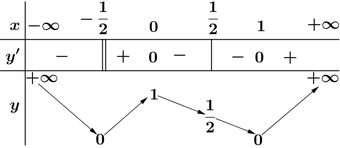
Dựa vào bảng biến thiên suy ra phương trình 
có bốn nghiệm phân biệt 
khi và chỉ khi 
.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
có bảng biến thiên như sauKhi đó
|
f
(
x
)
|
m
có bốn nghiệm phân biệt
x
1
x
2...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d có bảng biến thiên như sau
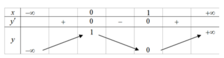
Khi đó | f ( x ) | = m có bốn nghiệm phân biệt x 1 < x 2 < x 3 < 1 2 < x 4 khi và chỉ khi
A. 0 < m ≤ 1
B. 1 2 < m < 1
C. 1 2 ≤ m < 1
D. 0 < m < 1
1.Tìm nghiệm đa thức
1)6x3 - 2x2
2)|3x + 7| + |2x2 - 2|
2.Chứng minh đa thức ko có nghiệm
1)x2 + 2x + 4
2)3x2 - x + 5
3.Tìm các hệ số a, b, c, d của đa thức f(x) = ax3 + bx2+ cx + d
Biết f(0)=5; f(1)=4; f(2)=31; f(3)=88
Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
Đúng 0
Bình luận (0)
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.
Đúng 0
Bình luận (0)
Bài 3:
$f(0)=a.0^3+b.0^2+c.0+d=d=5$
$f(1)=a+b+c+d=4$
$a+b+c=4-d=-1(*)$
$f(2)=8a+4b+2c+d=31$
$8a+4b+2c=31-d=26$
$4a+2b+c=13(**)$
$f(3)=27a+9b+3c+d=88$
$27a+9b+3c=88-d=83(***)$
Từ $(*); (**); (***)$ suy ra $a=\frac{1}{3}; b=13; c=\frac{-43}{3}$
Vậy.......
Đúng 1
Bình luận (0)
Biết phương trình
a
x
3
+
b
x
2
+
c
x
+
d
0
a
≠
0
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
y
a
x
3
+
b
x
2
+
c...
Đọc tiếp
Biết phương trình a x 3 + b x 2 + c x + d = 0 a ≠ 0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số y = a x 3 + b x 2 + c x + d có bao nhiêu điểm cực trị?
A. 4
B. 5
C. 6
D. 3
21 tháng 7 2021 lúc 12:29
Tìm các số tự nhiên a, b sao cho:
P= x4+ax3+bx2-8x+1
là bình phương của 1 đa thức
Cho đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình
a
x
3
+
b
x
2
+
c
x
+
d
m
có 3 nghiệm phân biệt. A.
m
2
B.
m...
Đọc tiếp
Cho đồ thị hàm số y = a x 3 + b x 2 + c x + d có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình a x 3 + b x 2 + c x + d = m có 3 nghiệm phân biệt.
A. m > 2
B. m < - 2
C. - 2 < m < 2
D. m = 2 m = - 2
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
Đúng 0
Bình luận (0)