Đáp án B
Ta có 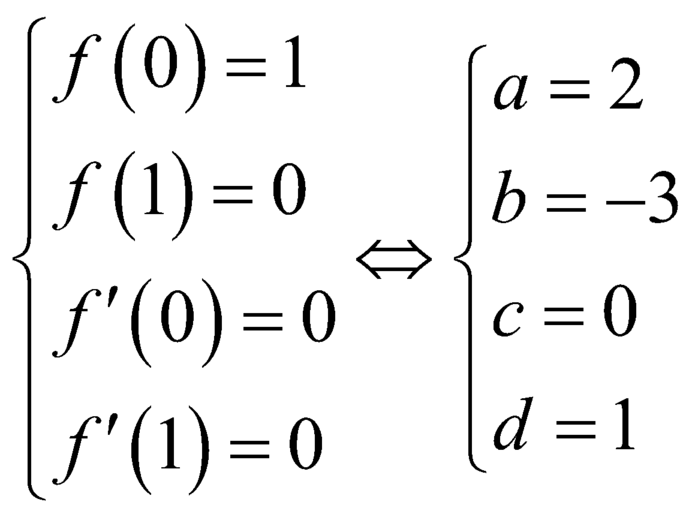
suy ra ![]() .
.
Ta có: 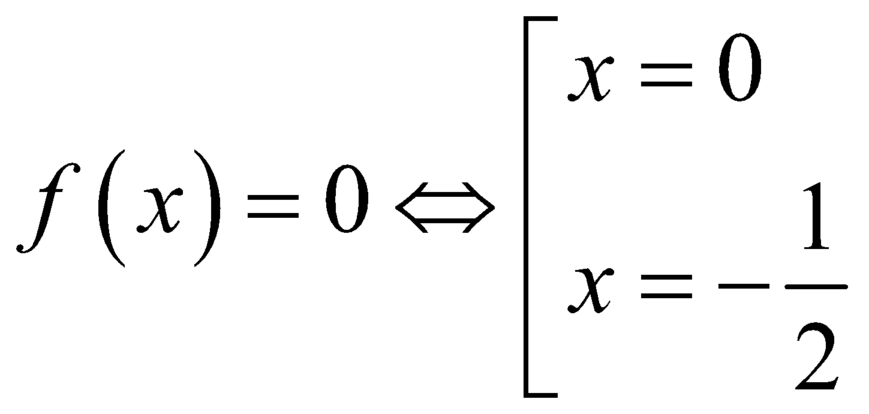 .
.
Bảng biến thiên của hàm số ![]() như sau:
như sau:
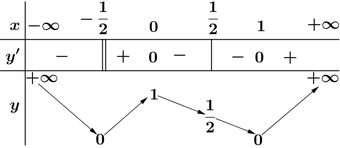
Dựa vào bảng biến thiên suy ra phương trình ![]() có bốn nghiệm phân biệt
có bốn nghiệm phân biệt ![]() khi và chỉ khi
khi và chỉ khi ![]() .
.
Đáp án B
Ta có 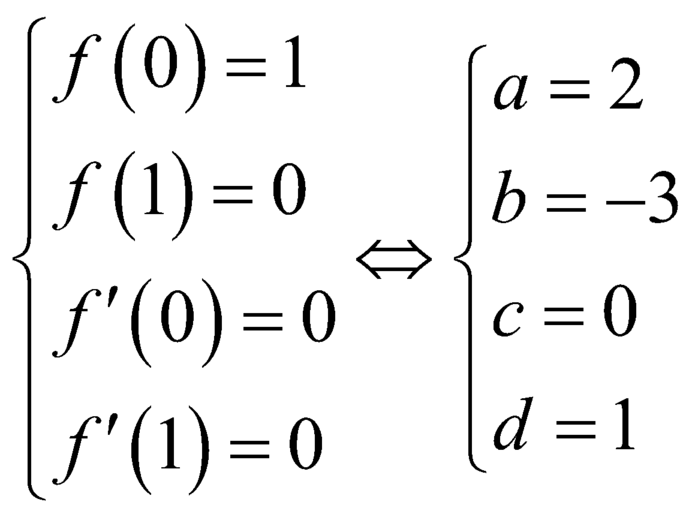
suy ra ![]() .
.
Ta có: 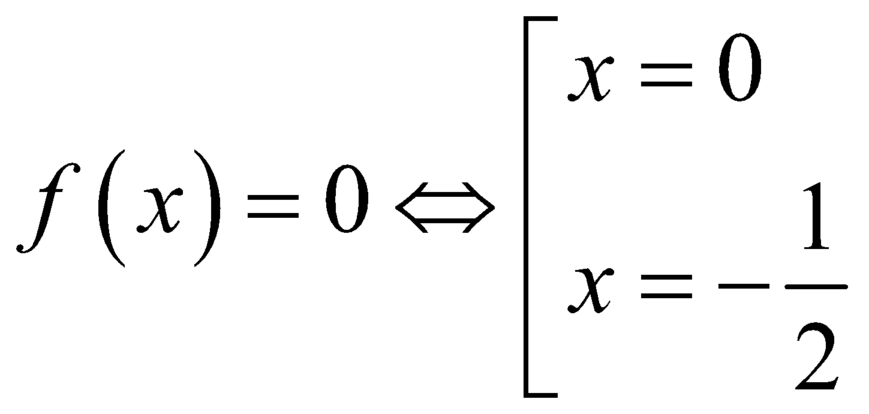 .
.
Bảng biến thiên của hàm số ![]() như sau:
như sau:

Dựa vào bảng biến thiên suy ra phương trình ![]() có bốn nghiệm phân biệt
có bốn nghiệm phân biệt ![]() khi và chỉ khi
khi và chỉ khi ![]() .
.
Cho hàm số y= f(x )= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
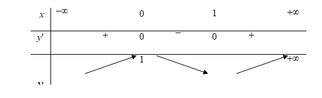
Khi đó |f(x)| = m có 4 nghiệm phân biệt x 1 < x 2 < x 3 < 1 2 < x 4 khi và chỉ khi
A. ½< m< 1
B. 0< m
C. m> 1
D. m< 1/2
Cho hàm số y= f(x) Hàm số y= f’(x) có bảng biến thiên như sau
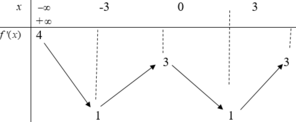
Bất phương trình f ( x ) < 3 e x + 2 + m có nghiệm x ∈ ( - 2 ; 2 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên như hình bên
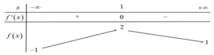
Phương trình f(x) = m có hai nghiệm thực phân biệt khi và chỉ khi
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) xác định và liên tục trên khoảng - ∞ ; + ∞ , có bảng biến thiên như sau:

Phương trình 2f(x) + m =0 có nghiệm phân biệt khi và chỉ khi
A. m ∈ - 4 ; 2
B. m ∈ - 4 ; 8
C. m ∈ - 8 ; 4
D. m ∈ - 2 ; 4
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
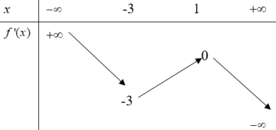
Bất phương trình
m
+
e
f
(
x
)
<
e
x
có nghiệm ![]() khi và chỉ khi
khi và chỉ khi
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f (x) có bảng biến thiên như sau:
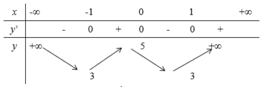
Tìm m để phương trình f (x) = 2 – 3m có bốn nghiệm phân biệt
A. m < - 1 h o ặ c m > - 1 3
B. - 1 < m < - 1 3
C. m = - 1 3
D. m ≤ - 1
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
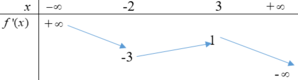
Bất phương trình f ( e x ) < e x + m nghiệm đúng với mọi x ∈ ( - 1 ; 1 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) có bảng biến thiên như sau
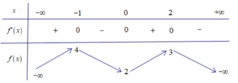
Bất phương trình x 2 + 1 f ( x ) ≥ m có nghiệm trên khoảng (-1;2) khi và chỉ khi
A. m<10
B. m ≤ 15
C. m<27
D. m<15
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau
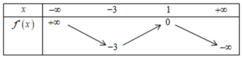
Bất phương trình f ( x ) < e x + m đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
![]()
![]()
![]()
![]()