Chứng minh rằng đường tròn nội tiếp và đường tròn Euler của một tam giác luôn tiếp xúc nhau.

Những câu hỏi liên quan
Cho tứ giác ABCD, các đường tròn nội tiếp hai tam giác ABC, ADC tiếp xúc nhau. Chứng minh rằng các đường tròn nội tiếp hai tam giác BAD, BCD tiếp xúc nhau.
Mỗi câu sau đây đúng hay sai?a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếpb) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếpc) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấyd) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.f) Giao điểm ba đường cao của một tam giác l...
Đọc tiếp
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp với đường tròn (O) , đường phân giác góc B^và C^ cắt đường tròn (O) tại D , E. Dựng đường tròn tâm D tiếp xúc với cạnh AC, đường tròn tâm E tiếp xúc với cạnh AB. Chứng minh rằng tâm của đường tròn nội tiếp tam giác ABC nằm trên tiếp tuyến chung của hai đường tròn (D) và (E).
Mỗi câu sau đây đúng hay sai ?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn nội tiếp tam giác ấy
e) Giao điểm ba đường phân giác của một tam giác là tâm đường tròn nội tiếp tam giác ấy
f) Giao điểm ba đường cao của một tam giá...
Đọc tiếp
Mỗi câu sau đây đúng hay sai ?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn nội tiếp tam giác ấy
e) Giao điểm ba đường phân giác của một tam giác là tâm đường tròn nội tiếp tam giác ấy
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy
g) Tứ giác có tổng độ dài các cặp cạnh đối bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó
Các câu đúng : a, d, e, g, h
Các câu sai : b, c, f, i
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn (O), có BE, CF là các đường cao. Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại T. EF cắt TC, TB lần lượt tại P, Q. Chứng minh rằng đường tròn ngoại tiếp tam giác TPQ tiếp xúc với (O).
Cho tam giác $ABC$ vuông tại $A$, nội tiếp trong đường tròn tâm $I$; bán kính $r$. Gọi $P$ là trung điểm của $AC$; $AH$ là đường cao của tam giác $ABC$.
a) Chứng minh tứ giác $APHI$ nội tiếp được trong đường tròn. Xác định tâm $K$ của đường tròn này.
b) Chứng minh hai đường tròn $(I)$ và $(K)$ tiếp xúc nhau.
oke bạn
Xem thêm câu trả lời
Cho tam giác ABC. D là tiếp điểm của đường tròn bàng tiếp góc A với BC.
a) Chứng minh rằng AB + BD = AC +CD.
b) Chứng minh rằng đường tròn bàng tiếp góc A của hai tam giác ADB và ADC tiếp xúc nhau.
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung
B
C
⏜
chứa A của (O). I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho
B
M
B
I
,
C
N
C
I
. Chứng m...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
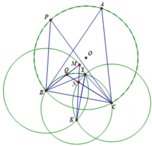
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.
Đúng 0
Bình luận (0)
Cho tam giác ABC (có ba góc nhọn) nội tiếp đường tròn (O) và tia phân giác của góc B cắt đường tròn tại M. Các đường cao BD và CK của ∆ABC cắt nhau tại H.
a) Chứng minh rằng tứ giác ADHK nội tiếp một đường tròn.
b) Chứng minh rằng OM là tia phân giác của góc AOC.
c) Gọi I là giao điểm của OM và AC. Tính tỉ số OI BH .
a,
Tứ giác ADHK có ˆADH+ˆAKH=90+90=180oADH^+AKH^=90+90=180o
⇒⇒ ADHK là tứ giác nội tiếp.
b,
BM phân giác ˆABCABC^
⇒ˆABM=ˆMBC⇒ABM^=MBC^
⇒⌢AM=⌢MC⇒AM⌢=MC⌢ (2 góc nội tiếp chắn 2 cung)
⇒ˆAOM=ˆMOC⇒AOM^=MOC^ (2 góc ở tâm cũng chắn 2 cung đó)
⇒⇒ OM phân giác ˆAOCAOC^

Đúng 1
Bình luận (0)











![♥╣[-_-]╠♥Minh Nèk(◍•ᴗ•◍)...](https://hoc24.vn/images/avt/avt16127090_256by256.jpg)




