Câu 4. a. Tính giá trị biểu thức b. Tìm y
455,29 – 73,2 x 5,4 1,8 x y = 65,16
Tính giá trị biểu thức
455,29 - 73,2 × 5,4
Tìm x
8× x = 8,6 × 10
455,29 - 73,2 x 5,4
= 455,29 - 395,28
= 60,01
\(8\times x=8,6\times10\)
\(8\times x=86\)
\(x=86:8\)
\(x=10,75\)
455,29 - 73,2 x 5,4
= 455,29 - 395,28
= 60,01
8×x=8,6×10
8×x=86
x=86:8
=10,75
Biết 2 đại lượng y và x tỉ lệ thuận với nhau khi x=6 thì y=8 a) Tìm hệ số tỉ lệ k của y đối với x b) Viết công thức biểu diễn y theo x c) Tính giá trị của y khi x=12 ;y=1,5 d) Tính giá trị của x khi y=10 ; y=5,4
`@` `\text {dnammv}`
`a,`
Vì `x` và `y` là `2` đại lượng tỉ lệ thuận `-> y=k*x`
Thay `x=6, y=8`
`-> 8=k*6`
`-> k=8/6`
`-> k=4/3`
Vậy, hệ số tỉ lệ `k=4/3`
`b,`
`y=4/3x`
`c,`
Khi `x=12 -> y=4/3*12=16`
`x=1,5` chứ nhỉ?
Khi `x=1,5 -> y=4/3*1,5=2`
`d,`
Khi `y=10 -> x=10 \div 4/3=7,5`
Khi `y=5,4 -> x=5,4 \div 4/3=4,05`
a: k=y/x=4/3
b: y=4/3x
c: Khi x=12 thì y=4/3*12=16
Khi x=1,5 thì 4/3*1,5=4/3*3/2=12/6=2
d: Khi y=10 thì 4/3x=10
=>x=10:4/3=30/4=15/2
Khi y=5,4 thì 4/3x=5,4
=>x=5,4:4/3=5,4*3/4=4,05
Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x=4 ; y=18 a) Tìm hệ số tỉ lệ nghịch của y đối với x b) Hãy biểu diễn y theo x c) Tính giá trị của y khi x=8 ; x=12 d) Tính giá trị của x khi y=10 ; y=5,4
a: k=xy=72
b: y=72/x
c: Khi x=8 thì y=72/8=9
Khi x=12 thì y=72/12=6
d: Khi y=10 thì x=72/10=7,2
Khi y=5,4 thì x=72/5,4=40/3
Tính giá trị biểu thức
a)397,5 : 7,5 X 10,5
b)36 : 15 X 5,4
a) 397,5 : 7,5 x 10,5 =53 x 10,5 = 556,5
b) 36 : 15 x 5,4 = 2,4 x 5,4 = 12,96
a. 53 x 10,5
= 556,5
b. 2,4 x 5,4
= 12,96
a)\(397,5\div7,5\times10,5\)
=53 \(\times\) 10,5
=556.5
b)36 \(\div\) 15 \(\times\) 5,4
=2,4 \(\times\) 5,4
=12,96
Câu 58: Cho biểu thức 2/3 - 4/3.x = 10/3 . Giá trị x là:
A. -2. B. 2. C. 4,6. D. 1,8.
Câu 58: Cho biểu thức 2/3 - 4/3.x = 10/3 . Giá trị x là:
A. -2. B. 2. C. 4,6. D. 1,8.
Phần II:Tự luận (7đ)
Câu Phần II:Tự luận (7đ)
Câu 1: a) Tính:
b) Cho biểu thức:
*) Tìm điều kiện xác định và rút gọn biểu thức A.
*) Tìm các giá trị của x để biểu thức A có giá trị âm.
Câu 2: Cho hai hàm số bậc nhất y = (m – 1)x + 2 với m ≠ 1 (d1)
y = (3 – m)x – 2 với m ≠ 3 (d2)
a/ Tìm giá trị của m để đồ thị của hai hàm số đã cho cắt
b/ Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ khi m = 0.
c/ Gọi I là giao điểm của hai đồ thị nói trên. Tìm tọa độ của điểm I (bằng phép toán).
d/ Tính góc hợp bởi đường thẳng (d2) với trục Ox khi m = 0.
Câu 3:Từ điểm M ở ngoài (O; R) vẽ hai tiếp tuyến MA, MB với (O) (A, B là 2
tiếp điểm), vẽ dây AC// OM.
a) Chứng minh OM AB tại H và suy ra OH.OM = R2.
b) MC cắt (O) tại E. Chứng minh 3 điểm B, O, C thẳng hàng và MH.MO = ME.MC.
c) Vẽ AK BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
1: a) Tính: ![]()

b) Cho biểu thức: 
*) Tìm điều kiện xác định và rút gọn biểu thức A.
*) Tìm các giá trị của x để biểu thức A có giá trị âm.
Câu 2: Cho hai hàm số bậc nhất y = (m – 1)x + 2 với m ≠ 1 (d1)
y = (3 – m)x – 2 với m ≠ 3 (d2)
a/ Tìm giá trị của m để đồ thị của hai hàm số đã cho cắt
b/ Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ khi m = 0.
c/ Gọi I là giao điểm của hai đồ thị nói trên. Tìm tọa độ của điểm I (bằng phép toán).
d/ Tính góc hợp bởi đường thẳng (d2) với trục Ox khi m = 0.
Câu 3:Từ điểm M ở ngoài (O; R) vẽ hai tiếp tuyến MA, MB với (O) (A, B là 2
tiếp điểm), vẽ dây AC// OM.
a) Chứng minh OM ![]() AB tại H và suy ra OH.OM = R2.
AB tại H và suy ra OH.OM = R2.
b) MC cắt (O) tại E. Chứng minh 3 điểm B, O, C thẳng hàng và MH.MO = ME.MC.
c) Vẽ AK![]() BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
BC tại K, gọi N là giao điểm của MC và AK. Chứng minh NA = NK
mọi người giúp mik với
Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
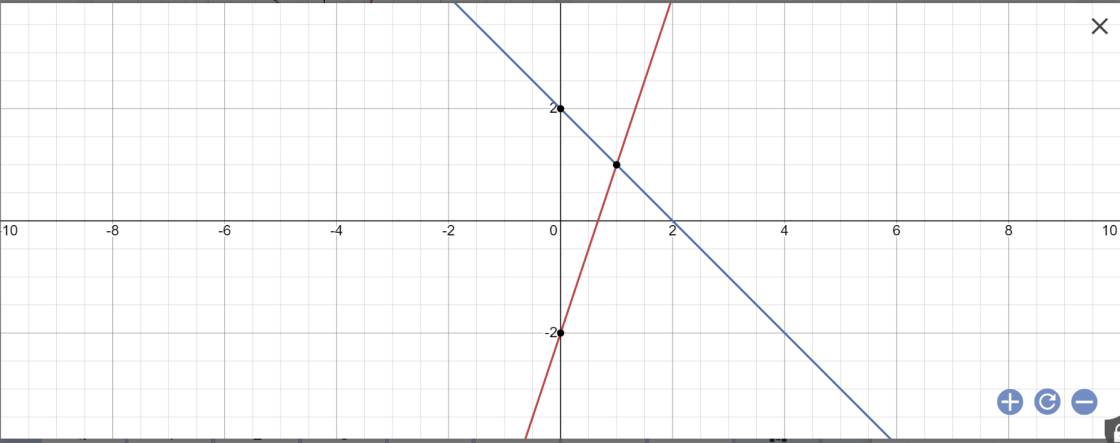
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)
Tính giá trị của biểu thức:
a) 101 – 0,36 : 3,6 x 1,8 + 8,96 = ?
b) 4,5 : (3,58 + 4,42) = ?
a) 101 – 0,36 : 3,6 x 1,8 + 8,96
= 101 – 2,6 x 1,8 + 8,98
= 101 – 4,68 + 8,96
= 96,32 – 8,96 = 87,36
b) 4,5 : (3,58 + 4,42)
= 4,5 : 8
= 0,5625
Tính giá trị của biểu thức.
a. 101 – 0,36 : 3,6 x 1,8 + 8,96 =
b. 4,5 : (3,58 + 4,42) =