a) Xét x = 0 => y = 1

Xét y = 0 => x = 1/3

b) Xét \(tan_{\alpha}=\dfrac{1}{\dfrac{1}{3}}=3=>\alpha=71^o33'\)

Để hàm số y=(2m-3)x-5m+1 là hàm số bậc nhất thì \(2m-3\ne0\)

\(\Leftrightarrow2m\ne3\)

\(\Leftrightarrow m\ne\dfrac{3}{2}\)

a) Để hàm số y=(2m-3)x-5m+1 đồng biến trên R thì \(2m-3>0\)

\(\Leftrightarrow2m>3\)

hay \(m>\dfrac{3}{2}\)

Vậy: Khi hàm số y=(2m-3)x-5m+1 đồng biến trên R thì \(m>\dfrac{3}{2}\)

b) Để đồ thị hàm số y=(2m-3)x-5m+1 song song với đường thẳng y=3x+5 thì \(\left\{{}\begin{matrix}2m-3=3\\-5m+1\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m=6\\-5m\ne4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne\dfrac{-4}{5}\end{matrix}\right.\Leftrightarrow m=3\left(nhận\right)\)

Vậy: Để đồ thị hàm số y=(2m-3)x-5m+1 song song với đường thẳng y=3x+5 thì m=3

a. Tìm m để hàm số đồng biến.

Để hàm số trên đồng biến. => 2m-3 > 0

                                          <=> 2m > 3

                                          <=> m > 3/2

b. Tìm m để đồ thị hàm số (1) song song đường thẳng y=3x-5 

Để đồ thị hàm số (1)  song song đường thẳng y = 3x - 5 

=>   2m-3 = 3 và -5m+1 khác  - 5

<=> m = 3      và m khác 6/5

<=> m = 3  (tm)

 c. Tính góc tạo bởi đường thẳng y=3x-5 với trục Ox

Gọi góc tạo bởi đường thẳng y=3x-5 với trục Ox là a (a>0)

=> tan a = |3| 

=> tan a = 3

=> góc a = 71^o 33'

a: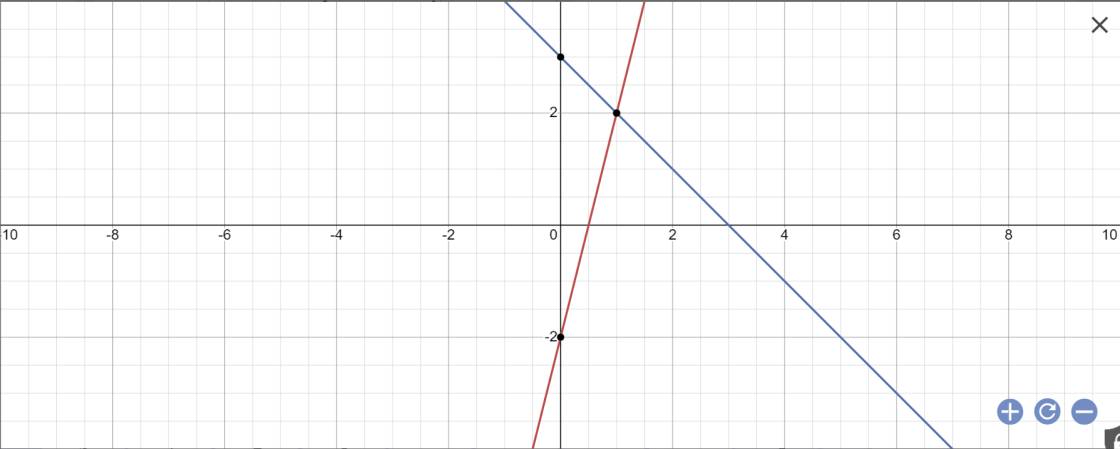 

b: Phương trình hoành độ giao điểm là:

4x-2=-x+3

=>4x+x=3+2

=>5x=5

=>x=1

Thay x=1 vào y=-x+3, ta được:

\(y=-1+3=2\)

Vậy: M(1;2)

c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox

(d1): y=4x-2

=>\(tan\alpha=4\)

=>\(\alpha=76^0\)

(d2): y=-x+3

=>\(tan\beta=-1\)

=>\(\beta=135^0\)

d: Thay y=6 vào (d1), ta được:

4x-2=6

=>4x=8

=>x=2

=>A(2;6)

Thay x=6/2=3 vào (d2), ta được:

\(y=-3+3=0\)

vậy: B(3;0)

Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:

\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)

Vậy: (d): y=-6x+18

e: A(2;6); B(3;0); M(1;2)

\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)

\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)

Chu vi tam giác AMB là:

\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)

Xét ΔAMB có 

\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)

=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)

Xét ΔAMB có

\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)

=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)

=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)

=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)

a: Vì (d)//y=2x+3 nên a=2

Vậy: y=2x+b

Thay x=1 và y=-2 vào (d), ta được:

b+2=-2

hay b=-4

Vậy: (d): y=2x-4

c: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}-4x+3=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{6}\\y=-\dfrac{5}{3}\end{matrix}\right.\)

d: Vì hai đường song song nên 2m-3=2

=>2m=5

hay m=5/2

1: (D): \(y=\left(m-2\right)x+1\)

(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)

Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\Leftrightarrow m=0\)

2:

a: Khi m=0 thì (D): \(y=\left(0-2\right)x+1=-2x+1\)

(D'): \(y=x\left(0^2-2\right)+0=-2x\)

b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox

(D): y=-2x+1

=>a=-2

\(tan\alpha=a=-2\)

=>\(\alpha\simeq116^034'\)

c: (D): y=-2x+1; (D'): y=-2x

Gọi A,B lần lượt là giao điểm của (D) với trục Ox và Oy

Ox\(\perp\)Oy nên OA\(\perp\)OB

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\-2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-2x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,5\\y=0\end{matrix}\right.\)

Vậy: A(0,5;0)

\(OA=\sqrt{\left(0,5-0\right)^2+\left(0-0\right)^2}=0,5\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-2x+1=-2\cdot0+1=1\end{matrix}\right.\)

vậy:B(0;1)

\(OB=\sqrt{\left(0-0\right)^2+\left(1-0\right)^2}=1\)

ΔOAB vuông tại O

=>\(OA^2+OB^2=AB^2\)

=>\(AB^2=1^2+0,5^2=1,25\)

=>\(AB=\sqrt{1,25}=\dfrac{\sqrt{5}}{2}\)

Chu vi tam giác OAB là: \(C_{OAB}=OA+OB+AB=1,5+\dfrac{\sqrt{5}}{2}=\dfrac{3+\sqrt{5}}{2}\)

Diện tích tam giác OAB là:

\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot1\cdot0,5=0,25\)

d: (D): y=-2x+1

=>2x+y-1=0

Khoảng cách từ O đến (D) là:

\(d\left(O;\left(D\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)

4: (D): y=(m-2)x+1

=mx-2x+1

Tọa độ điểm cố định mà (D) luôn đi qua là:

\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)

giải giúp mik vs 

a) 

Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3

Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1

Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)

Thay x=0 vào hàm số y= -x+1, ta được: y=  -0 + 1 = 1

Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1

(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)

b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :

3x+3 = -x+1

<=> 3x + x = 1 - 3

<=> 4x = -2

<=> x= - \(\dfrac{1}{2}\)

Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)

Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))

c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α

OB= \(\left|x_B\right|=\left|-1\right|=1\)

OC= \(\left|y_C\right|=\left|3\right|=3\)

Xét △OBC (O= 90*), có:

\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)

=> α= 71*34'

Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'

1: Khi m=2 thì y=(2-1)x+2=x+2

Vẽ đồ thị:

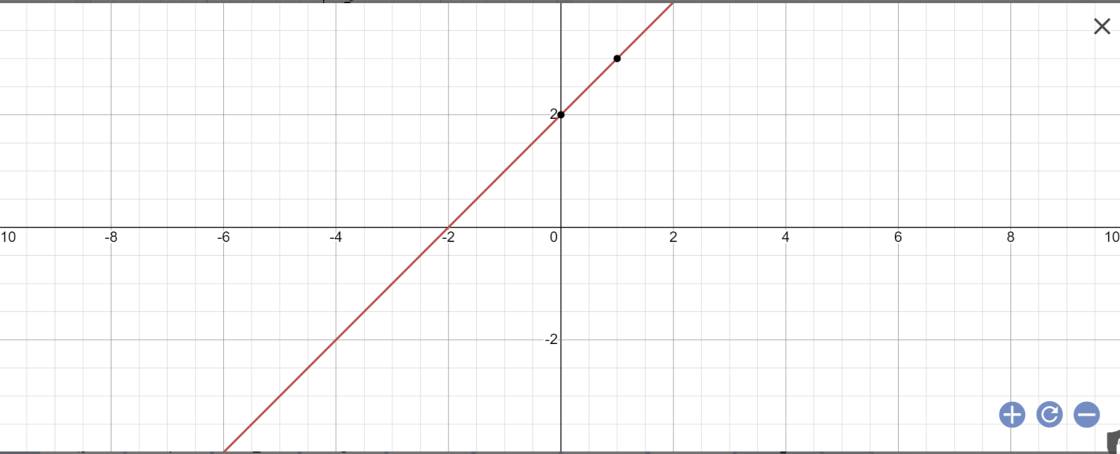
\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

2: Thay x=1 và y=0 vào (d), ta được:

\(1\left(m-1\right)+m=0\)

=>2m-1=0

=>m=1/2

3:

y=(m-1)x+m

=mx-x+m

=m(x+1)-x

Điểm mà (d) luôn đi qua có tọa độ là:

\(\left\{{}\begin{matrix}x+1=0\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)