Cho tam giác ABC tìm điểm N sao cho véctơ NA - vécto NB + vecto NC = 0

Những câu hỏi liên quan
cho tam giác ABC : a)tìm các điểm M và N sao cho vector MA - vector MB + vector MC = vector 0 và 2 vector NA + vector NB + vector NC = vector 0
a: \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{0}\)
=>\(\overrightarrow{BA}=\overrightarrow{CM}\)
=>BAMC là hình bình hành
=>M là điểm thỏa mãn BAMC là hình bình hành
Gọi K là trung điểm của BC
\(2\overrightarrow{NA}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\overrightarrow{NA}+2\overrightarrow{NK}=\overrightarrow{0}\)
=>\(\overrightarrow{NA}+\overrightarrow{NK}=\overrightarrow{0}\)
=>N là trung điểm của AK
Đúng 0
Bình luận (0)
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC vectơ CA vectơ MB vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA vecto NB vectơ MC vectơ 0
Xem chi tiết
Cho tam giác ABC a,tìm điểm M thoả mãn điều kiện vectơ MC +vectơ CA +vectơ MB =vectơ 0 b,tìm N thoả mãn điều kiện vectơ NA- vecto NB+ vectơ MC= vectơ 0
Xem chi tiết
shsbdudjwosmgs
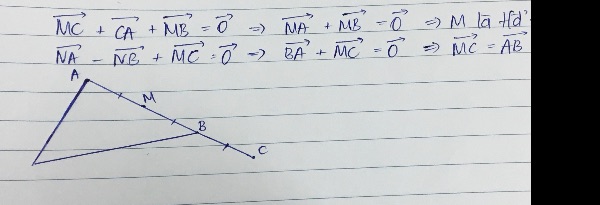
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có : A(3,1) B(5,3) C(-1,1)
a) chứng tỏ tam giác ABC vuông cân
b) Tìm toạ độ của điểm M biết vecto MA - 2 vecto MB + 4 vecto MC = vector 0
c) tính diện tích tam giác ABC
d) Tìm N thuộc Oy để NB + NC nhỏ nhất
Cho tam giác ABC . Gọi M , N , P là 3 điểm thoả mãn vecto MC = 1/3 vecto MB , vecto NA + 3 vecto NC = 0 , vecto PA + vecto PB = 0 a ) Biểu diễn vecto MP , vecto NP theo hai vecto AB và AC b ) Chứng minh 3 điểm M , N, P thẳng hàng
cho tam giác ABC : a)tìm các điểm M và N sao cho vector MA - vector MB + vector MC = vector 0 và 2 vector NA + vector NB + vector NC = vector 0
b) với các điểm M,N ở câu a), tìm các số p và q sao cho vector MN = p nhân vector AB + q nhân vector AC
a: 
b: \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}\)
\(=\overrightarrow{CB}+\dfrac{1}{2}\cdot\overrightarrow{AK}\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\dfrac{1}{2}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\overrightarrow{AC}+\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
\(=\dfrac{5}{4}\cdot\overrightarrow{AB}-\dfrac{3}{4}\cdot\overrightarrow{AC}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, gọi M,N,P lần lượt là trung điểm của BC, AC, AB. D là trung điểm của AM. Chứng minh rằng:
a, vecto AB+ vecto AC+ vecto MN+ vecto MP = vecto 0
b, vecto NB+ vecto NC - 2.vecto AN= 4.vecto ND
Cho tam giác đều ABC cạnh a. Gọi M là trung điểm của AB và N là hột điểm trên cạnh AC sao cho NC = 2 NA. a) Phân tích vecto MN theo hai vecto AB và AC. b) Gọi G là trọng tâm của tam giác ABC. Tinh CG.CAN theo a.
E cần gấp achij nào giúp e cho mai e nộp
Đúng 0
Bình luận (0)
a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a a) xác định điểm K thỏa mãn vecto KA+ vecto KB+ vecto KC+4vecto KD = vecto 0 b) tìm {M} thỏa mãn : | vecto MA+ vecto MB + vecto MC +4vecto MF| = 2a c) tìm {N} thỏa mãn : |2 vecto NA- vecto NB + vecto NC | = | vecto ND +vecto NC|
Cho tan giác ABC đều cạnh a, I là điểm trên cạnh BC sao cho BC 3BI và J là trung điểm của AB.
a) Tính |vecto AB + vecto AC|
b) Chứng minh vecto AI 2/3vecto AB + 1/2vecto AC.
c) Gọi M là điểm thoả : 3vecto MA + vecto MB - 2vecto MC vecto 0.
d) Gọi N là điểm thoả : |vecto NA + vecto NB| |vecto NB + vecto NC. Chứng minh điểm N thuộc một đường thẳng cố định.
giúp mình với ạ :((
Đọc tiếp
Cho tan giác ABC đều cạnh a, I là điểm trên cạnh BC sao cho BC = 3BI và J là trung điểm của AB.
a) Tính |vecto AB + vecto AC|
b) Chứng minh vecto AI = 2/3vecto AB + 1/2vecto AC.
c) Gọi M là điểm thoả : 3vecto MA + vecto MB - 2vecto MC = vecto 0.
d) Gọi N là điểm thoả : |vecto NA + vecto NB| = |vecto NB + vecto NC. Chứng minh điểm N thuộc một đường thẳng cố định.
giúp mình với ạ :((












