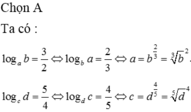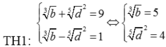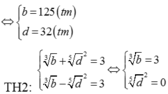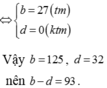cho a là 1 số nguyên dương biết a100 =1. Khi đó a=......

Những câu hỏi liên quan
Bài 1 : Tìm các số nguyên a , b biết tích của chúng là 24 và tổng của 2 số đó là - 40
Bài 2 : CMR với mọi số nguyên a ta có ( a - 1 ) * ( a + 2 ) +12 không chia hết cho 9 và không là bội của 9
Bài 3 : Cho dãy a1 ; a2 ; a3 ; ... ; a160 . Trong đó a1 = 1 ; a2 = -1 ; ak = ak - 2 * ak - 1 ( K thuộc số tự nhiên ; K nhỏ hơn hoặc bằng 3 ) . Tính a100
Câu 1:
cho 100 số nguyên dương a1, a2,... a100 thỏa mãn:
\(\frac{1}{a1^2}+\frac{1}{a2^2}+...+\frac{1}{a100^2}=\frac{199}{100}\)
chứng minh: trong 100 số a1, a2,... a100 đã cho tồn tại ít nhất 2 số bằng nhau.
Giả sử trong 100 số nguyên dương đã cho không tồn tại 2 số nào bằng nhau
Không mất tính tổng quát, giả sử \(a_1< a_2< a_3< ...< a_{100}\)
\(\Rightarrow a_1\ge1;a_2\ge2;a_3\ge3;....;a_{100}\ge100\Rightarrow\frac{1}{a_1^2}+\frac{1}{a_2^2}+\frac{1}{a^2_3}...+\frac{1}{a^2_{100}}\le\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}\left(1\right)\)
Lại có: \(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=\frac{199}{100}\left(2\right)\)
Từ (1) và (2) => \(\frac{1}{a_1^2}+\frac{1}{a^2_2}+...+\frac{1}{a^2_{100}}< \frac{199}{100}\) trái với giả thiết
Vậy tồn tại ít nhất 2 số bằng nhau trong 100 số a1,a2,...,a100
Đúng 0
Bình luận (0)
1) Biết A = 945 + 360 + 972 + 225 + x chia hết cho 45. Khi đó số dư khi chia x cho 5 là ...
2) Một số tự nhiên n có 54 ước nguyên dương. Khi đó tích các ước nguyên dương của n là n^x . Vậy x = ...
1. Tính:
A 2100 - 299 -298 - 297 - ......- 22 - 2 - 1
2. Cho dãy số: a1 ; a2 ; a3 ;.....; a100. Trong đó: a1 1 ; a2 -1 ; ak ak-2 . ak-1
( k thuộc N ; k lớn hơn hoặc bằng 3 )
3. Tính các số nguyên x ; y biết:
a) ( x + 1) ( x - 2 ) 0
b) ( x - 2 ) ( y - 2 ) 5
Đọc tiếp
1. Tính:
A= 2100 - 299 -298 - 297 - ......- 22 - 2 - 1
2. Cho dãy số: a1 ; a2 ; a3 ;.....; a100. Trong đó: a1 = 1 ; a2 = -1 ; ak= ak-2 . ak-1
( k thuộc N ; k lớn hơn hoặc bằng 3 )
3. Tính các số nguyên x ; y biết:
a) ( x + 1) ( x - 2 ) = 0
b) ( x - 2 ) ( y - 2 ) = 5
F
x
là một nguyên hàm của hàm số
f
x
3
x
2
+
1
2
x
+
1
.
Biết
F
0
0
,
F
1
a
+
b
c
ln
3
,...
Đọc tiếp
F x là một nguyên hàm của hàm số f x = 3 x 2 + 1 2 x + 1 . Biết F 0 = 0 , F 1 = a + b c ln 3 , trong đó a, b, c là các số nguyên dương và b c là phân số tối giản. Khi đó giá trị biểu thức a + b + c bằng
A. 4
B. 3
C. 12
D. 9
Đáp án A.
Ta có
F x = ∫ 3 x 2 + 1 2 x + 1 d x = x 3 + 1 2 ln 2 x + 1 + C
mà F 0 = 0 ⇒ C = 0
Do đó
F x = x 3 + 1 2 ln 2 x + 1 ⇒ F 1 = 1 + 1 2 ln 3 ⇒ a = 1 ; b = 1 ; c = 2 ⇒ a + b + c = 4 .
Đúng 0
Bình luận (0)
1,Cho 2000 số A1,A2,A3,...A2000 là các số TN thỏa mãn: 1/A1+1/A2+1/A3+....+1/A20001. CMR tồn tại ít nhất 1 số Ak là số chẵn2,Gọi A1,A2,A3,...A100 là các số TN thỏa mãn: 1/A21+1/A22+....+1/A1002199/100. CMR có ít nhất 2 số TN trong các số trên nhau3,Cho 2021 số nguyên dương A1,A2,....,A2021 thỏa mãn 1/A1+1/A2+1/A3+.....+1/A20211011. CMR ít nhất 2 trong đó nhauGiúp mình với nha!
Đọc tiếp
1,Cho 2000 số A1,A2,A3,...A2000 là các số TN thỏa mãn: 1/A1+1/A2+1/A3+....+1/A2000=1. CMR tồn tại ít nhất 1 số Ak là số chẵn
2,Gọi A1,A2,A3,...A100 là các số TN thỏa mãn: 1/A21+1/A22+....+1/A1002=199/100. CMR có ít nhất 2 số TN trong các số trên =nhau
3,Cho 2021 số nguyên dương A1,A2,....,A2021 thỏa mãn 1/A1+1/A2+1/A3+.....+1/A2021=1011. CMR ít nhất 2 trong đó = nhau
Giúp mình với nha!
Cho dãy số a1 (a với số 1 ở dưới ạ) , a2, a3, ......, a100 trong đó a1 = 1; a2= -1;ak= ak-2 ak-1 (k thuộc N, k lớn hơn hoặc bằng 3). Tính a100?
Cho a,b,c,d là các số nguyên dương,
a
≠
1
;
c
≠
1
thỏa mãn
log
a
b
3
2
,
log
c
d
5
4
và
a
-
c
9
. Khi đó
b
-
d
A.93 B.9 C.13 D.21
Đọc tiếp
Cho a,b,c,d là các số nguyên dương,
a ≠ 1 ; c ≠ 1 thỏa mãn log a b = 3 2 ,
log c d = 5 4 và a - c = 9 . Khi đó b - d
A.93
B.9
C.13
D.21
Cho a, b, c, d là các số nguyên dương,
a
≠
1
;
c
≠
1
thỏa mãn
log
a
b
3
2
;
log
c
d
5
4
và
a
−
c
9
. Khi đó b – d bằng A. 93 B. 9 C. 13 D. 21
Đọc tiếp
Cho a, b, c, d là các số nguyên dương, a ≠ 1 ; c ≠ 1 thỏa mãn log a b = 3 2 ; log c d = 5 4 và a − c = 9 . Khi đó b – d bằng
A. 93
B. 9
C. 13
D. 21