cho đường tròn tâm O bằng đường kính BC bằng 12R vẽ dây AB bằng R a.tính các cạnh và các góc của tam giác ABC b.kẻ dây AD vuông góc OR tại H tính độ dài dây AB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O;R) có đường kính BC và cạnh ABR. Kẻ dây AD vuông góc với BC tại Ha) Tính độ dài các cạnh AC,AH và số đo góc B, góc Cb) Chứng minh: AH.HDHB.HCc) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, căt AC ở N. Chứng minh: C,D,N thẳng hàngd) Chứng minh: AI là tiếp tuyến của đường tròn (O) và tính AI theo R
Đọc tiếp
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O;R) có đường kính BC và cạnh AB=R. Kẻ dây AD vuông góc với BC tại H
a) Tính độ dài các cạnh AC,AH và số đo góc B, góc C
b) Chứng minh: AH.HD=HB.HC
c) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, căt AC ở N. Chứng minh: C,D,N thẳng hàng
d) Chứng minh: AI là tiếp tuyến của đường tròn (O) và tính AI theo R
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=\left(2\cdot R\right)^2-R^2=3\cdot R^2\)
\(\Leftrightarrow AC=R\cdot\sqrt{3}\)(đvđd)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot2R=R\cdot R\sqrt{3}\)
hay \(AH=\dfrac{R\sqrt{3}}{2}\)(đvđd)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{R\sqrt{3}}{2\cdot R}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{ABC}=60^0\)
Xét ΔABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^0\)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(AC=R\cdot\sqrt{3}\) đvđd; \(AH=\dfrac{R\sqrt{3}}{2}\)đvđd; \(\widehat{ABC}=60^0\); \(\widehat{ACB}=30^0\)
b) Xét (O) có
BC là đường kính của (O)(gt)
AD là dây của đường tròn(O)
BC⊥AD tại H(gt)
Do đó: H là trung điểm của AD(Định lí đường kính vuông góc với dây)
⇔AH=HD
hay \(AH\cdot HD=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(2)
Từ (1) và (2) suy ra \(AH\cdot HD=HB\cdot HC\)(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R) có BC là đường kính và ACR. Kẻ dây AD vuông góc với BC tại H.
1) Tính độ dài các cạnh AB, AH theo R;
2) Chứng minh rằng HA.HDHB.HC;
3) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, cắt AB ở N. Chứng minh ba điểm N, C, D thẳng hàng;
4) Chứng minh AI là tiếp tuyến của đường tròn (O, R).
Đọc tiếp
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R) có BC là đường kính và AC=R. Kẻ dây AD vuông góc với BC tại H.
1) Tính độ dài các cạnh AB, AH theo R;
2) Chứng minh rằng HA.HD=HB.HC;
3) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, cắt AB ở N. Chứng minh ba điểm N, C, D thẳng hàng;
4) Chứng minh AI là tiếp tuyến của đường tròn (O, R).
1) Vì BC là đường kính của (O) nên BC=2R
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=\left(2R\right)^2-R^2=3R^2\)
hay \(AB=R\sqrt{3}\)(đvđd)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot2R=R\cdot R\sqrt{3}\)
\(\Leftrightarrow AH=\dfrac{R^2\cdot\sqrt{3}}{2\cdot R}=\dfrac{R\sqrt{3}}{2}\)(đvđd)
Vậy: \(AB=R\sqrt{3}\); \(AH=\dfrac{R\sqrt{3}}{2}\)
2) Xét (O) có
OC là một phần đường kính
AD là dây
OC⊥AD tại H
Do đó: H là trung điểm của AD(Định lí đường kính vuông góc với dây)
⇒\(HA=HD=\dfrac{AD}{2}\)
hay \(HA\cdot HD=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(2)
Từ (1) và (2) suy ra \(HA\cdot HD=HB\cdot HC\)(đpcm)
Đúng 1
Bình luận (1)
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB 6,tgB4/3.Tính cạnh BC.
Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng.
Câu3:Hai đường tròn (O;R)và O;R)d.Biết R12cm,R7cm,d4 thì vị trí tương đối của 2 đường tròn là?
Câu4:Cho hàm số y(2m-1)x+3
a)Tìm m.để HS đi qua điểm A(2;5)
b)Vẽ đths vs m tìm đc ở câu a
Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyế...
Đọc tiếp
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB =6,tgB=4/3.Tính cạnh BC. Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng. Câu3:Hai đường tròn (O;R)và O';R')=d.Biết R=12cm,R'=7cm,d=4 thì vị trí tương đối của 2 đường tròn là? Câu4:Cho hàm số y=(2m-1)x+3 a)Tìm m.để HS đi qua điểm A(2;5) b)Vẽ đths vs m tìm đc ở câu a Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyến MA,MB với đường tròn.Gọi H là trung điểm của CD,OM cắt AB tại E.CMR a)AB vuông góc với OM b)Tích OE.OM ko đổi c)Khi M di chuyển trên đường thẳng d thì đường thẳng AB đi qua 1 điểm cố định. (Mọi người giúp e vs ạ)
Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)
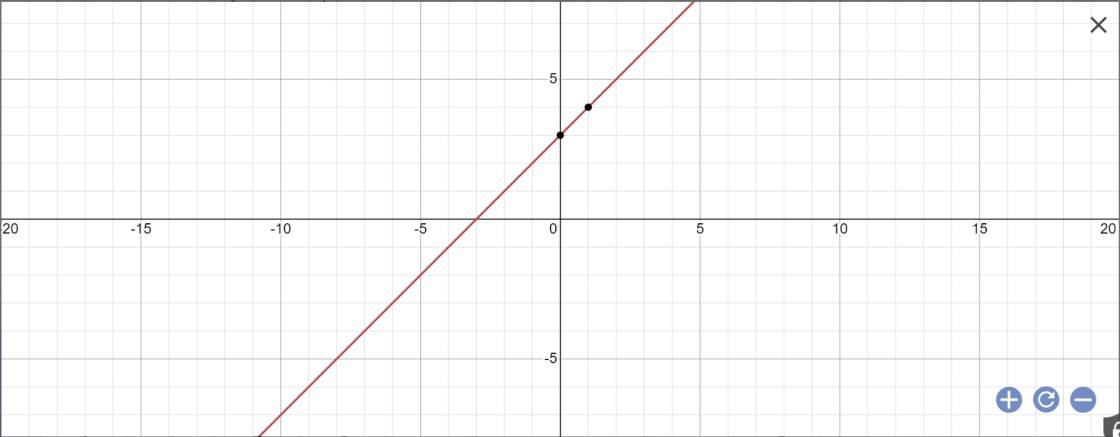
Đúng 1
Bình luận (0)
Cho đường tròn tâm O đường kính AB = 10cm, vẽ dây BC = 6cm. Vẽ dây CD vuông góc với AB tại I.
a) Chứng minh tam giác ABC vuông tại C.
b) Tính độ dài AC, CD.
cho nửa đường tròn tâm o đường kính bc . tính độ dài AC và số đo góc của tam giác ABC biêt a) Dây AB=R√3 b) Dây AB=R√2
Cho tam giác ABC vuông tại A, đường tròn tâm O đường kính AB cắt BC tại H. a) Chứng minh: AH vuông góc với BC và AB2 BC. BH b)Vẽ dây AD của đường tròn (O) vuông góc với OC. Chứng minh: CD là tiếp tuyến của đường tròn (O). c) Kẻ DK vuông góc với AB tại K. DK cắt BC tại I. Chứng minh: I là trung điểm của DK. giải giúm mình plssss
Đọc tiếp
Cho tam giác ABC vuông tại A, đường tròn tâm O đường kính AB cắt BC tại H.
a) Chứng minh: AH vuông góc với BC và AB2 = BC. BH
b)Vẽ dây AD của đường tròn (O) vuông góc với OC. Chứng minh: CD là tiếp tuyến của đường tròn (O).
c) Kẻ DK vuông góc với AB tại K. DK cắt BC tại I. Chứng minh: I là trung điểm của DK.
giải giúm mình plssss
a: Xet (O) có
ΔAHB nội tiếp
AB là đường kính
Do đo: ΔAHB vuông tại H
=>AH vuông góc với BC
AB^2=BC*BH
b: ΔOAD cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOD
Xét ΔOAC và ΔODC có
OA=OD
góc AOC=góc DOC
OC chung
Do đó: ΔOAC=ΔODC
=>góc ODC=90 độ
=>CD là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
cho đường tròn (O;R) , đường kính AB, dây cung BC=R
Tính độ dài các cạnh và giá trị các góc của tam giác ABC
Cho tam giác ABC vuông tại A, đường tròn tâm O đường kính AC cắt BC tại K , vẽ dây cung AD của đường tròn tâm O vuông góc với BO tại H. Cm: Góc AKB = 90 độ
Cho tam giác ABC vuông tại A, đường tròn tâm O đường kính AB cắt BC tại H.
a) Chứng minh: AH vuông góc với BC và AB2 BC. BH
b)Vẽ dây AD của đường tròn (O) vuông góc với OC. Chứng minh: CD là tiếp tuyến của đường tròn (O).
c) Kẻ DK vuông góc với AB tại K. DK cắt BC tại I. Chứng minh: I là trung điểm của DK.
Đọc tiếp
Cho tam giác ABC vuông tại A, đường tròn tâm O đường kính AB cắt BC tại H.
a) Chứng minh: AH vuông góc với BC và AB2 = BC. BH
b)Vẽ dây AD của đường tròn (O) vuông góc với OC. Chứng minh: CD là tiếp tuyến của đường tròn (O).
c) Kẻ DK vuông góc với AB tại K. DK cắt BC tại I. Chứng minh: I là trung điểm của DK.
Bài 1:Cho đường tròn (O;R), đường kính AB, dây cung BCR
a, Tính các cạnh và các góc chưa biết của tam giác ABC theo R
b, Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) ở D
CM: OD là đường trung trực của AC
tam giác ADC là hình gì? Vì sao?
c, CM: DC là tiếp tuyến của đường tròn (O)
d, Đường thẳng OD cắt đường tròn (O) tại I. Cm: I là tâm đường tròn nội tiếp tam giác ADC
Đọc tiếp
Bài 1:Cho đường tròn (O;R), đường kính AB, dây cung BC=R
a, Tính các cạnh và các góc chưa biết của tam giác ABC theo R
b, Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) ở D
CM: OD là đường trung trực của AC
tam giác ADC là hình gì? Vì sao?
c, CM: DC là tiếp tuyến của đường tròn (O)
d, Đường thẳng OD cắt đường tròn (O) tại I. Cm: I là tâm đường tròn nội tiếp tam giác ADC
b) Gọi OD ⊥ AC tại I ( I thuộc OD)
Có: OD⊥ AC (gt) và CB⊥ AC ( △ABC vuông tại C)
Do đó OD // CB
Xét △ABC, có:
OD// CB (cmt)
O là trung điểm AB ( AB là đường kính)
Do đó OI là đường trung bình ABC
=>I là trung điểm AC
Có: OD ⊥ AC(gt) , I trung điểm AC (cmt) (I thuộc OD)
Nên OD là đường trung trực của AC
c)
Xét t/giác AOC, có:
AO=OC (=R)
Do đó t/giác AOC cân tại O
Mà OI ⊥ AC
Nên OI cũng là đường phân giác góc AOC
=> AOI = COI
Xét t/giác ADO và t/giác DOC, có:
OD chung
AOI = COI (cmt)
OA=OC (=R)
Do đó t/giác ADO = t/giác CDO (c-g-c)
=> DAO = DCO
Mà DAO= 90
Nên DCO = 90
Có C thuộc (O) ( dây cung BC)
Nên CD là tiếp tuyến
Đúng 2
Bình luận (1)
a) Xét △ABC, có:
AB là đường kính của (O) (gt)
Do đó △ABC vuông tại C
Xét ABC (C=90), có:
+\(AC^2+CB^2=AB^2\left(Pytago\right)\) \(^{ }\Rightarrow AC^2=AB^2-CB^2\)
=> AC = \(R\sqrt{3}\)
+ \(sin_A=\dfrac{CB}{AB}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow A=30^o\)
+ A + B = 90 (△ABC vuông tại C)
30 + B = 90
B = 90 - 30
B= 60
Đúng 1
Bình luận (0)
b) Gọi OD ⊥ AC tại I ( I thuộc OD)
Có: OD⊥ AC (gt) và CB⊥ AC ( △ABC vuông tại C)
Do đó OD // CB
Xét △ABC, có:
OD// CB (cmt)
O là trung điểm AB ( AB là đường kính)
Do đó OI là đường trung bình ABC
=>I là trung điểm AC
Có: OD ⊥ AC(gt) , I trung điểm AC (cmt) (I thuộc OD)
Nên OD là đường trung trực của AC
c)
Xét t/giác AOC, có:
AO=OC (=R)
Do đó t/giác AOC cân tại O
Mà OI ⊥ AC
Nên OI cũng là đường phân giác góc AOC
=> AOI = COI
Xét t/giác ADO và t/giác DOC, có:
OD chung
AOI = COI (cmt)
OA=OC (=R)
Do đó t/giác ADO = t/giác CDO (c-g-c)
=> DAO = DCO
Mà DAO= 90
Nên DCO = 90
Có C thuộc (O) ( dây cung BC)
Nên CD là tiếp tuyến
Đúng 0
Bình luận (0)
Xem thêm câu trả lời













