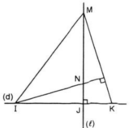
l ⊥ d tại J, và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.

N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.

IN và MJ cắt nhau tại N .

Theo tính chất ba đường cao của ta giác ⇒ N là trực tâm của ΔMKI.

⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.

Vậy KN ⏊ IM

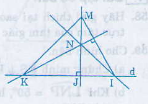
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

Vì NJ ⊥ IK, KM ⊥ NI nên NJ và KM là hai đường cao của tam giác IKN.

Hai đường cao này giao nhau tại điểm M nên M là trực tâm của tam giác IKN.

Do đó, theo tính chất trực tâm của tam giác, IM là đường cao thứ ba của tam giác đó, hay KN⊥ IM.

Cũng có thể kết luận như sau:  KN là đường cao thứ ba của ΔMIK hay NK ⊥ IM (đpcm).

Nối M với I ta được ΔMIK.

Trong ΔMIK có: MJ ⊥ IK (do l ⊥ d) và IN ⊥ MK

Do đó N là trực tâm của ΔMIK.

Suy ra KN là đường cao thứ ba của ΔMIK hay NK ⊥ IM (đpcm).

Nối M với I ta được ΔMIK.

Trong ΔMIK có: MJ ⊥ IK (do l ⊥ d) và IN ⊥ MK

Do đó N là trực tâm của ΔMIK.

Suy ra KN là đường cao thứ ba của ΔMIK hay KN ⊥ IM (đpcm).

tiếng việt???

đây mà là tiếng việt à ?

Giải tương tự như bài tập 59

∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

Hướng dẫn:

Giải tương tự như bài tập 59

∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

Nối M với I ta được ΔMIK.

Trong ΔMIK có: MJ ⊥ IK (do l ⊥ d) và IN ⊥ MK

Do đó N là trực tâm của ΔMIK.

Suy ra KN là đường cao thứ ba của ΔMIK hay NK ⊥ IM (đpcm).

gọi giao điểm của IN và MK là H.Xét tam giác IMK:

+IHvuông góc với MK

+MJ vuông góc với IK

mà 2 đường này cắt nhau tại N

=>KN vuông góc với IM(3 đường cao đồng quy tại 1 điểm)

Giải tương tự như bài tập 59

∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

gọi giao điểm của IN và MK là H.Xét tam giác IMK:

+>IHvuông góc với MK

+>MJ vuông góc với IK

mà 2 đường này cắt nhau tại N

=>KN vuông góc với IM(3 đường cao đồng quy tại 1 điểm)