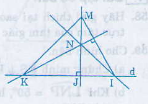
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK
Cho tam giác ABC đều trên cạnh BC lấy điểm E bất kì đường thẳng vuông góc với AC kẻ từ E cắt đường thẳng vuông góc với AB kẻ từ B tại D lấy trung điểm K của đoạn EC trên tia đối của tia KD lấy điểm F sao cho KD=FK
Từ E kẻ đường thẳng song song với AB cắt AC tại M gọi G là tọng tâm của tam giác CME và I là trung điểm của đoạn MB tính góc AIG
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh BC, trên tia đối của tia CB lấy điểm E sao cho CE=BD. Các đường thẳng vuông góc với BC tại D và E lần lượt cắt các đường thẳng AB và Ac theo thứ tự tại M, N. Gọi I là giao điểm của MN với BC. CMR đường thẳng vuông góc với MN luôn đi qua một điểm cố đinh.
Cho tam giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA ở K. Chứng minh rằng AK = AC
Đề nghị trợ giúp, xin cảm ơn: Cho đường tròn đường kính CD, tâm I. Tại C và D kẻ hai tiếp tuyến Cx và Dy với đường tròn tâm I. Lấy điểm M trên CD, A trên Dy. Dựng đường tròn tâm O ngoại tiếp tam giác ADM cắt đường tròn tâm I tại E khác D. DO cắt đường tròn tâm O tại F. Kẻ DE cắt Cx tại K. Chứng minh rằng MK vuông góc với CA.
Cho ΔABC có góc A=90o . Kẻ AH vuông góc với BC tại H . Trên cạnh BC lấy D sao cho BD = BA . Đường vuông góc với BC tại D cắt AC ở E.
a) So sánh AE và DE
b) Chứng minh tia AD là tia phân giác của góc HAC
c) Đường phân giác của góc ngoài đỉnh C cắt đường thẳng BE ở K . Tính góc BAK
=> Mọi người giúp mk nha
3) Cho tam giác ABC có BC<AB, đường phân giác BDcvaf đường rtung tuyến BM (M, D thuộc AC) Đường thẳng qua C vuông góc với BD tại E cắt BM,BA làn lược tại I và K Chứng minh rằng ID// BC
Cho tam giác ABC có góc A=90 độ, AB=AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. CMR AK=AC.
Trong mặt phẳng (P) cho đường tròn (C) có đường kính A B = 2 . Trên đường thẳng vuông góc với (P) tại điểm A, lấy điểm S sao cho S A = 5 . Xét điểm M thay đổi trên (C), mặt phẳng (α) qua A vuông góc với SB, lần lượt cắt SB, SM tại H và K. Diện tích tam giác AHK đạt giá trị lớn nhất bằng
A. 5 9
B. 2
C. 4 5
D. 1
Trong không gian cho hai đường thẳng chéo nhau d và △ , vuông góc với nhau và nhận AB=a làm đoạn vuông góc chung A ∈ d , B ∈ △ . Trên d lấy điểm M, trên △ lấy điểm N sao cho AM=2a, BN=4a. Gọi I là tâm mặt cầu ngoại tiếp tứ diện ABMN. Khoảng cách giữa hai đường thẳng AM và BI là
A. 4 a 17 17
B. a
C. 4 a 5
D. 2 a 2 3
