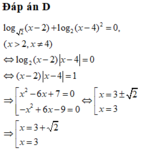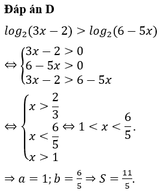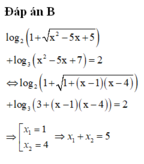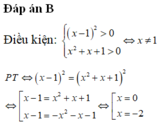Tổng các nghiệm của phương trình log2 (x² - 2) + Log1/2 (5x - 8 )= 0 Ghi cách giải hộ mk ạ

Những câu hỏi liên quan
Tổng các nghiệm của phương trình
log
2
(
x
-
2
)
+
log
2
(
x
-
4
)
2
0
bằng A. 9 B.
3
+
2
C. 12 D.
6...
Đọc tiếp
Tổng các nghiệm của phương trình log 2 ( x - 2 ) + log 2 ( x - 4 ) 2 = 0 bằng
A. 9
B. 3 + 2
C. 12
D. 6 + 2
Giải bất phương trình
l
o
g
2
(
3
x
-
2
)
l
o
g
2
(
6
-
5
x
)
được tập nghiệm là (a;b). Hãy tính tổng Sa+b A. S 26/5 B. S 8/5 C. S 28/15 D. S 11/5
Đọc tiếp
Giải bất phương trình l o g 2 ( 3 x - 2 ) > l o g 2 ( 6 - 5 x ) được tập nghiệm là (a;b). Hãy tính tổng S=a+b
A. S= 26/5
B. S= 8/5
C. S= 28/15
D. S= 11/5
Giải bất phương trình
log
2
(
3
x
-
2
)
log
2
(
6
-
5
x
)
được tập nghiệm là (a;b). Hãy tính tổng Sa+b A.
S
8
3
B.
S
28
15...
Đọc tiếp
Giải bất phương trình log 2 ( 3 x - 2 ) > log 2 ( 6 - 5 x ) được tập nghiệm là (a;b). Hãy tính tổng S=a+b
A. S = 8 3
B. S = 28 15
C. S = 11 5
D. S = 31 6
Tổng các nghiệm phương trình
log
2
(
1
+
x
2
-
5
x
+
5
)
+
log
3
(
x
2
-
5
x
+
7
)...
Đọc tiếp
Tổng các nghiệm phương trình log 2 ( 1 + x 2 - 5 x + 5 ) + log 3 ( x 2 - 5 x + 7 ) = 2 là
A. 3
B. 5
C. 6
D. 2
Giải các phương trình sau
a, x^2+ 3x + 2=0
b, 2x^2 - 5x + 3=0
Hộ Mk giải vs ạ
x.(2x^2+5x-3)=0
x.(2x^2-x+6x-3)=0
x.(2x-1).(x+3)=0
-> x=0 hoặc x=-3 hoặc x=1/2
Đúng 0
Bình luận (0)
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để bất phương trình log2( 5x - 1) .log2)( 2.5x - 2) > m - 1 có nghiệm x ≥ 1?
A. m ≥ 7
B. m > 7
C. m ≤ 7
D. m < 7
Bất phương trình
log
2
(
3
x
−
2
)
log
2
(
6
−
5
x
)
có tập nghiệm là (a;b). Tổng a + b bằng A.
8
3
.
B.
28
15
.
C.
26
5
....
Đọc tiếp
Bất phương trình log 2 ( 3 x − 2 ) > log 2 ( 6 − 5 x ) có tập nghiệm là (a;b). Tổng a + b bằng
A. 8 3 .
B. 28 15 .
C. 26 5 .
D. 11 5 .
Tổng các nghiệm của phương trình
log
2
(
x
-
1
)
2
2
log
2
(
x
2
+
x
+
1
)
là: A. 9. B. -2 C. 1 D. 0
Đọc tiếp
Tổng các nghiệm của phương trình log 2 ( x - 1 ) 2 = 2 log 2 ( x 2 + x + 1 ) là:
A. 9.
B. -2
C. 1
D. 0
Tổng các nghiệm của phương trình log 2 ( x - 1 ) 2 = 2 log 2 ( x 2 + x + 1 ) là
A. 9
B. -2
C. 1
D. 0