Cho tam giác ABC cân tại A. Kẻ các đường phân giác BD và CE, M là trung điểm của BC
a) AM là đường phân giác của BAC
b) Ba đường phân giác BD, CE, AM đồng quy
Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Kẻ các tia phân giác BD, CE. Lấy M là trung điểm của BC.
a) Chứng minh AM là tia phân giác của góc BAC.
b) Ba đường thẳng AM, BD, CE đồng quy tại H.
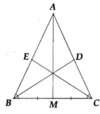
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A đường trung tuyến AM và đường phân giác BD cắt nhau tại K gọi là giao điểm của CK và AB Chứng minh rằng BD=CE giúp với ạ
Các đường phân giác BD và CE cắt nhau tại K nên AK la đường phân giác của góc A.
Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến, do đó AK đi qua trung điểm M của BC.
Các đường phân giác BD và CE cắt nhau tại K nên AK là đường phân giác của góc A .
Trong 1 tam giác cân , đường phân giác xuất phát từ đỉnh đồng thời là đường trunh tuyến , do đó AK đi qua trung điểm M của BC .
25 tháng 4 2023 lúc 21:58
cho tam giác ABC góc A=90 độ đường cao AH, phân giác BD (D thuộc AC)
a) CM tam giác BAH đồng dạng với tam giác BCA và góc BAH =góc BAC b,gọi I là giao điểm của AH và BD CM: BI.BC=BA.BD
c, kẻ CE vuông góc BD cắt BA tại M .CM: AI song song với MD và BA.BM+CE.CM=BC^2
mn ơi cứu mik với mik
a: Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng vói ΔBCA
b: Xét ΔBAD và ΔBHI có
góc BAD=góc BHI
góc ABD=góc HBI
=>ΔBAD đồng dạng vói ΔBHI
=>BA/BH=BD/BI
=>BA*BI=BH*BD
Đúng 2
Bình luận (0)
Cho tam giác ABC có M là trung điểm của BC. Dựng các hình bình hành ABCD và ACBE. Chứng minh: a) Ba đường thẳng AM, BD, CE đồng quy b) Ba đường thẳng AM, CD, BE đồng quy
1) Cho tam giác ABC (BC>BA) phân giác BD trên BC lấy M sao cho BM bằng BA
a )CM : DM = DA
b) N là giao điểm của AB và DM. CM : tam giác ABC bằng tam giác MBN
c)CM: AM // NC
2) Cho tam giác ABC có BA = BC kẻ đường phân giác CD của góc C, từ P kẻ đường vuông góc vs CD, đường thẳng này cắt các đường thẳng AB, BC tại E và F.CMR :
a) tam giác CEP cân
b)DA = 1/ 2 CE
Cho tam giác ABC cân tại A; hai đường trung tuyến CE và BD giao nhau tại G.
a) Chứng minh tam giác ABD= tam giác ACE; BD= CE.
b) Chứng minh tia AG là phân giác của góc A
c) Gọi K là trung điểm của AG; I là trung điểm của CG. Chứng minh BD; CK; AI đồng quy.
a)Xét tam giác ABD và tam giác ACE,ta có:
A là góc chung
AB=AC(ví tam giác ABC cân tại A)
AE=AD(gt)
=> tam giác ABD=tam giác ACE(c.g.c)=>BD=CE( 2 cạnh tương ứng)
b)Vì BD,CE lần lượt là đường trung tuyến mà lại giao nhau tại G(mà BD=CE)=>GE=GD=1/3 BD=1/3 CE
=>EG=GD
Xét tam giác AEG và tam giác ADG ,ta có:
GE=GD(c/m trên)
AE=AD(gt)
AG cạnh chung
=>tam giác AEG=tam giác ADG(c.c.c)
=>góc EAG=góc DAG=>AG là tia p/g góc A
c)Ta có: Vì K là trung điểm AG;I là trung điểm GC và AD=DC
=>AI;CK:GD lần lượt là đường trung tuyến tam giác AGC=>BD;CK;AI đồng quy(t/c 3 đường trung tuyến của tam giác)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A,kẻ các tia p/g BD,CE,gọi MD là trung điểm
a) C/M AM là tia p/g của góc BAC
b) C/M 3 đg thẳng hàng AM,BD,CE đồng quy tại h
Sửa đề: M là trung điểm của BC
a: ΔABC cân tại A có AM là trung tuyến
nên AM là phân giác của góc BAC
b: Xét ΔABC có
AM,BD,CE là các đường phân giác
=>AM,BD,CE đồng quy tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. Lấy M là trung điểm BC.
a) Chứng minh tam giác ABM = tam giác ACM và tia AM là tia phân giác của góc BAC
b) Lấy điểm D thuộc tia đối của tia BC và điểm E thuộc tia đối của tia CB sao cho BD = CE. Kẻ BH vuông góc với AD tại H, kẻ CI vuông góc với AE tại I. Chứng minh: tam giác ABD = tam giác ACE; DH = EI.
c) Trong trường hợp BA = BD và góc BAC = 90 , tính góc BDA
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đo: ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔABD và ΔACE co
AB=AC
góc ABD=góc ACE
BD=CE
Do đo: ΔABD=ΔACE
Xét ΔBHD vuông tại H và ΔCIE vuông tại I có
BD=CE
góc D=góc E
Do đo: ΔBHD=ΔCIE
=>DH=EI
Đúng 1
Bình luận (0)
Câu 7. Cho tam giác MNP cân tại M. Tia phân giác của góc NMP cắt NP tại A.
a) Chứng minh tam giác AMN = tam giác AMP.
b) Kẻ AB vuông góc với MN, AC vuông góc với MP. Chứng minh tam giác ABC
cân.
c) Chứng minh AM vuông góc với BC
d) Kẻ BD vuông góc với NA tại D. Gọi E là giao điểm của đường thẳng BD và MP.
Chứng minh M là trung điểm của CE.