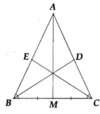
a) Chứng minh được ∆ A M B = ∆ A M C (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC.
b) Xét tam giác ABC có AM, BD,CE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng AM,BD,CE đồng quy.
Bài 3. (3,0 điểm) Cho tam giác ABC cân tại A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. Gọi M là trung điểm của BC.
a) Chứng minh rằng tam giác ADE là tam giác cân.
b) Chứng minh AM là tia phân giác của góc DAE.
c) Kẻ BH ⊥ AD và CK ⊥ AE. Chứng minh BH = CK.
d) Chứng minh ba đường thẳng AM, BH và CK đồng quy
Cho tam giác ABC cân tại A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. Gọi M là trung điểm của BC.
a) Chứng minh rằng tam giác ADE là tam giác cân.
b) Chứng minh AM là tia phân giác của góc DAE.
c) Kẻ BH ⊥ AD và CK ⊥ AE. Chứng minh BH = CK.
d) Chứng minh ba đường thẳng AM, BH và CK đồng quy.
cho tam giác ABC cân tại A,kẻ các tia p/g BD,CE,gọi MD là trung điểm
a) C/M AM là tia p/g của góc BAC
b) C/M 3 đg thẳng hàng AM,BD,CE đồng quy tại h
Cho tam giác ABC . Kẻ trung tuyến AM. Trên tia đối của tia MA lấy điểm E sao cho ME = MA a)Cm tam giác ABM = tam giác ECM b)Kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA Chứng minh BC là tia phân giác của góc ABD và BD = CE c) Hai đường thẳng BD và CE cắt nhau tại K . Chứng Minh Tam góc BCK cân
Cho tam giác ABC có AB = AC. Lấy M là trung điểm BC.
a) Chứng minh tam giác ABM = tam giác ACM và tia AM là tia phân giác của góc BAC
b) Lấy điểm D thuộc tia đối của tia BC và điểm E thuộc tia đối của tia CB sao cho BD = CE. Kẻ BH vuông góc với AD tại H, kẻ CI vuông góc với AE tại I. Chứng minh: tam giác ABD = tam giác ACE; DH = EI.
c) Trong trường hợp BA = BD và góc BAC = 90 , tính góc BDA
Cho tam giác ABC cân tại A, trung tuyến AM. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE.
a) Chứng minh tam giác ADE cân tại A
b) Chứng minh AM là tia phân giác D A E ^ .
c) Kẻ B H ⊥ A D , C K ⊥ A E với H ∈ A D , K ∈ A E . Chứng minh D B H ^ = E C K ^
d) Gọi N là giao điểm của HB và KC. Chứng minh ba điểm A, M, N thẳng hàng.
Cho tam giác ABC cân tại A. Đường trung tuyến AM. Trên tia đối của tia BC lấy D, trên tia đối CB lấy E sao cho BD = CE
a: Tam giác ADE cân tại A
b: AM là tia phân giác
c: kẻ BH vuông góc AD ,CK vuông góc AE .Chứng minh tam giác AHB=tam giác AKC
d:CM: HK// DE
e: gọi N là giao điểm của HB và CK .Chứng minh AB vuông góc ID
f:CM: HB,AM,CK cùng đi qua điểm I
Cho tam giác ABC cân tại A .Trên tia đối của các tia BC và CB thứ tự lấy các điểm D và E sao cho BD=CE 1) Chứng minh tam giác ADE là tam giác cân 2)Gọi M là trung điểm của BC . Chứng minh AM là tia phân giác của góc DAE 3) Từ B và C kẻ BH và CK thứ tự vuông góc với AD và AE. Chứng minh BH=CK cùng đi qua một điểm
Cho tam giác ABC . Kẻ trung tuyến AM. Trên tia đối của tia MA lấy điểm E sao cho ME = MA
a)Cm tam giác ABM = tam giác ECM
b)Kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HD = HA Chứng minh BC là tia phân giác của góc ABD và BD = CE
c) Hai đường thẳng BD và CE cắt nhau tại K . Chứng Minh Tam gíac BCK cân
