Tìm m để d // d' câu 2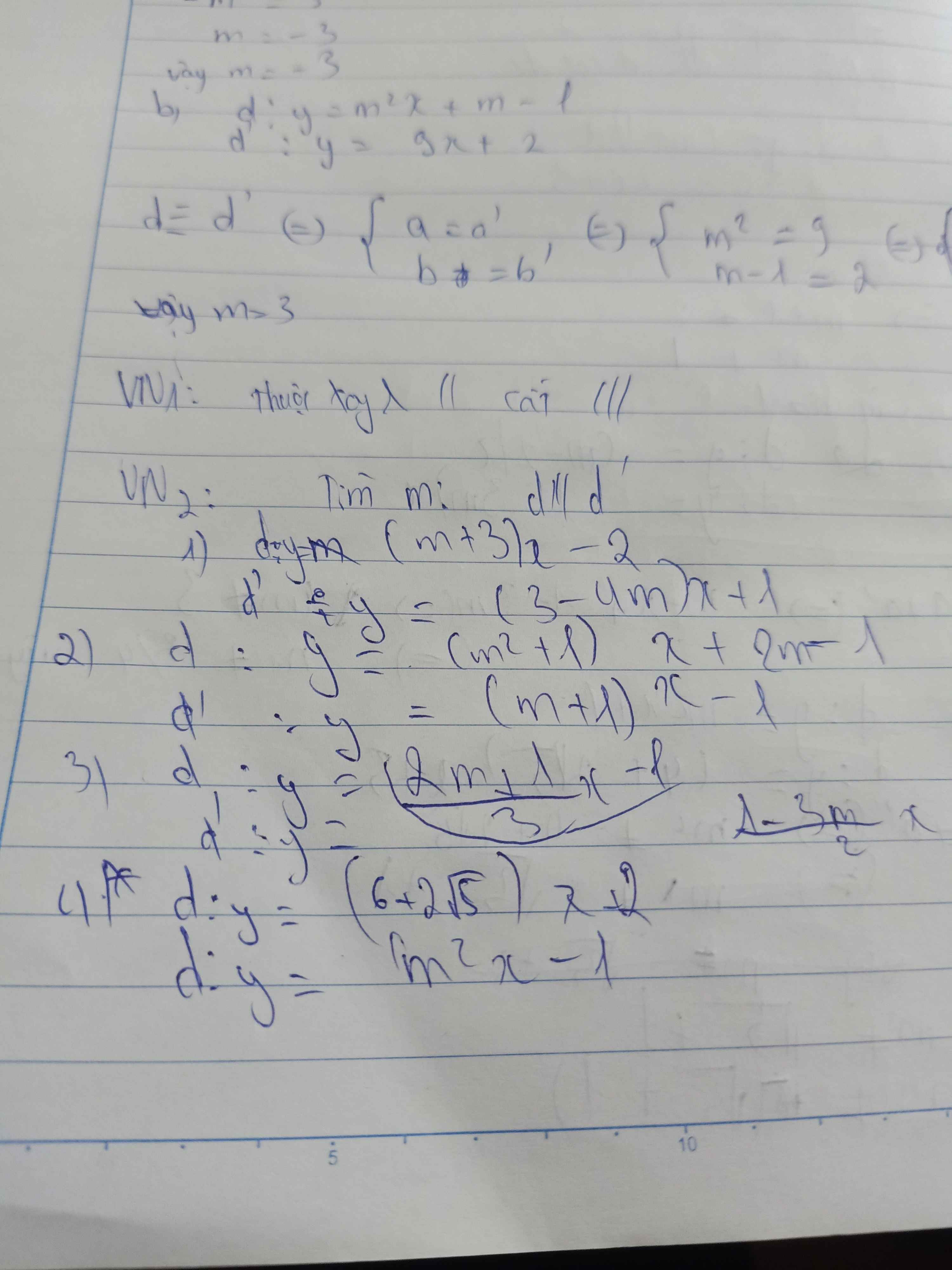

Những câu hỏi liên quan
Làm cho mik câu d chi tiết được ko ạ !!!
2:Cho các hàm số: y = (m-2)x +3m -1 (d)(Với m khác 2)
a) Tìm m để(d) cắt trục tung tại điểm có tung độ bằng 2.
b)Tìm m để hệ số góc của (d) là -2.
c)Tìm m để đường thẳng(d) song song với (d1): y =3x -2.
d)Tìm m để đường thẳng(d) cắt (d2): y =3x + 2 tại một điểm nằm bên trái trục tung.
a: Thay x=0 và y=2 vào (d), ta được:
3m-1=2
hay m=1
Đúng 1
Bình luận (1)
Cho (d) y=(m-2)x+3 (m khác 2)
(d') y=-m^2x+1
a) Tìm m để d//d'
b) Tìm m để d cắt Ox tại A, cắt Oy tại B sao cho góc BAO=60 độ.
Em cần câu b ạ, em cảm ơn ạ.
a) Để (d)//(d') thì \(-m^2=m-2\)
\(\Leftrightarrow-m^2-m+2=0\)
\(\Leftrightarrow m^2-m-2=0\)
\(\Leftrightarrow\left(m-2\right)\left(m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-1\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Bài 15. Cho hàm số y (m-2)x+3 có đô thị là đường thẳng (d)a ) Tim m để hàm số đồng biến, nghịch biến.b) Tìm m để (d) đi qua điểm A(1; 2)c) Tìm m để (d) song song với đường thàng yx ..d) Vẽ (d) với m vừa tìm được ở câu c. Tìm tọa độ giao điểm của đô thị hàm số vừa vẽ với đường thẳng y 2x+1. (VẼ HÌNH HỘ MIK Ạ )e) Tim điểm cố định mà (d) luôn đi qua với mọi mf) Tim m để khoảng cách từ gốc tọa độ o đến (d) bằng 1.GIÚP VỚI TỐI NAY MIK PHẢI NỘP LUN RỒI
Đọc tiếp
Bài 15. Cho hàm số y= (m-2)x+3 có đô thị là đường thẳng (d)
a ) Tim m để hàm số đồng biến, nghịch biến.
b) Tìm m để (d) đi qua điểm A(1; 2)
c) Tìm m để (d) song song với đường thàng y=x ..
d) Vẽ (d) với m vừa tìm được ở câu c. Tìm tọa độ giao điểm của đô thị hàm số vừa vẽ với đường thẳng y= 2x+1. (VẼ HÌNH HỘ MIK Ạ )
e) Tim điểm cố định mà (d) luôn đi qua với mọi m
f) Tim m để khoảng cách từ gốc tọa độ o đến (d) bằng 1.
GIÚP VỚI TỐI NAY MIK PHẢI NỘP LUN RỒI
Câu 1: Cho hai đường thẳng (d):y=mx+1 và (d'):y=m2x +m+1, trong đó m là tham số. Tìm m để (d) và (d') song song với nhau
Câu 2: Cho phương trình: x2-2mx+m2+2m+2=0 (m là tham số). Tìm m để phương trình đã cho có 2 nghiệm phân biệt x1, x2 thỏa mãn \(\dfrac{2}{x_1}+\dfrac{2}{x_2}=x_1+x_2\)
Cho đồ thị (d): y=mx+4
a)Tìm m để (d) song song với (d'):y=-2x-3
b)Tìm m để (d) tạo với 2 trục tọa độ 1 tam giác co diện tích là 8
Giải giúp em câu b ạ
b) Gọi giao điểm của (d) với Ox là điểm A. \(\Rightarrow y=0.\)
\(\Rightarrow\) \(OA=\left|\dfrac{-4}{m}\right|=\dfrac{4}{\left|m\right|}.\) (đvđd).
Gọi giao điểm của (d) với Oy là điểm B. \(\Rightarrow x=0.\)
\(\Rightarrow OB=4\) (đvđd).
Ta có: \(S_{\Delta ABC}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\dfrac{4}{\left|m\right|}.4=8\) (đvdt).
\(\Rightarrow\dfrac{4}{\left|m\right|}=4.\Leftrightarrow\left|m\right|=1.\Leftrightarrow\left[{}\begin{matrix}m=1.\\m=-1.\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho hàm số y=(m-1)x+5
a,tìm m để (d) đi qua A (1,2)
b,với m vừa tìm được ở câu a hàm số đã cho đồng biến hay nghịch biến
c,tìm m để (d) song song với đường thẳng y=x+2
d,tìm tọa độ giao điểm của (d) và (d') :y=2x+2 khi m=4
a) Để (d) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào (d), ta được:
\(m-1+5=2\)
\(\Leftrightarrow m+4=2\)
hay m=-2
Vậy: m=-2
Đúng 0
Bình luận (0)
Câu 1: Cho 2 hàm số y = 3x ( d) và y = ( 𝑚2 − 1)𝑥 + 𝑚 − 2 ( d’) với m là
số thực cho trước. Tìm giá trị của m để (d’ ) song song với ( d )
A. m = - 2.
B. m = 2.
C. m = 4.
D. m ≠ 2 .
Câu 3 (2,0 điểm). Cho hàm số y = (m - 2) x + 2 với m khác 2 có đồ thị là đường thẳng (d)
b) Tìm m để đường thẳng (d) song song với đường thẳng (d1) : y = - 5x + 1
c) Đường thẳng (d) cắt trục Ox tại điểm A, cắt trục Oy tại điểm B. Tìm giá trị của m để diện tích tam giác ABO bằng 1
Em cần gấp ạ
b: Để (d)//(d1) thì m-2=-5 và 2<>1(đúng)
=>m=-3
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-2\right)x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{-2}{m-2}\end{matrix}\right.\)
=>\(OA=\dfrac{2}{\left|m-2\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)\cdot0+2=2\end{matrix}\right.\)
=>OB=2
\(S_{OAB}=1\)
=>\(\dfrac{1}{2}\cdot OA\cdot OB=1\)
=>\(\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-1\right|}=1\)
=>\(\left|m-1\right|=2\)
=>\(\left[{}\begin{matrix}m-1=2\\m-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.1 Cho hàm sốbậc nhấty = (m -2)x +2 ( tham sốm; m≠2) có đồthị(d)a/ Vẽ(d) khi m = 0b/ Tìm m để(d) song song với đường thẳngy = -3x +1c/ Tìm m đểkhoảng cách từgốc tọa độO đến (d) =2/5 Mình cần câu c thôi , giúp mk nhé .
b: Để hai đồ thị song song thì m-2=-3
hay m=-1
Đúng 0
Bình luận (0)
# Bài 24. Cho hai đường thẳng (D): y (m − 2)x + 1& (D0 ) : y m2 x − 2x + m. 1) Tìm m để (D) là hàm số bậc nhất? Hàm số đồng biến? Hàm số nghịch biến? 2) Tìm m biết (D) // (D’). 3) Với m tìm được ở câu 2 hãy a) Vẽ đồ thị (D); b) Tính góc tạo bởi đường thẳng (D) và trục Ox; c) Tính chu vi và diện tích tam giác được tạo bởi đường thẳng (D), Ox, Oy; d) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (D). 4) Cho hai đường thẳng (d1) y 2x−8 và (d2) y −x+1. Tìm m để đường thẳng (D),(d1),(d2) đồng...
Đọc tiếp
# Bài 24. Cho hai đường thẳng (D): y = (m − 2)x + 1& (D0 ) : y = m2 x − 2x + m. 1) Tìm m để (D) là hàm số bậc nhất? Hàm số đồng biến? Hàm số nghịch biến? 2) Tìm m biết (D) // (D’). 3) Với m tìm được ở câu 2 hãy a) Vẽ đồ thị (D); b) Tính góc tạo bởi đường thẳng (D) và trục Ox; c) Tính chu vi và diện tích tam giác được tạo bởi đường thẳng (D), Ox, Oy; d) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (D). 4) Cho hai đường thẳng (d1) y = 2x−8 và (d2) y = −x+1. Tìm m để đường thẳng (D),(d1),(d2) đồng quy. 5) Tìm m để (D) và (D’) cắt nhau tại một điểm nằm trên trục hoành. 6) Chứng minh rằng đường thẳng (D) luôn đi qua một điểm cố định khi m thay đổi. 7) Tìm m sao cho đường thẳng (D) tạo với hai trục Ox, Oy một tam giác có diện tích bằng 2. 8) Tìm m sao cho khoảng cách từ gốc tọa độ O đến đường thẳng (D) đạt giá trị lớn nhất.
1: (D): y=(m-2)x+1
(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)
Để (D) là hàm số bậc nhất thì m-2<>0
=>m<>2
Để (D): y=(m-2)x+1 đồng biến trên R thì m-2>0
=>m>2
Để (D): y=(m-2)x+1 nghịch biến trên R thì m-2<0
=>m<2
2: Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\)
=>m=0
3:
a: Khi m=0 thì (D): y=(0-2)x+1=-x+1
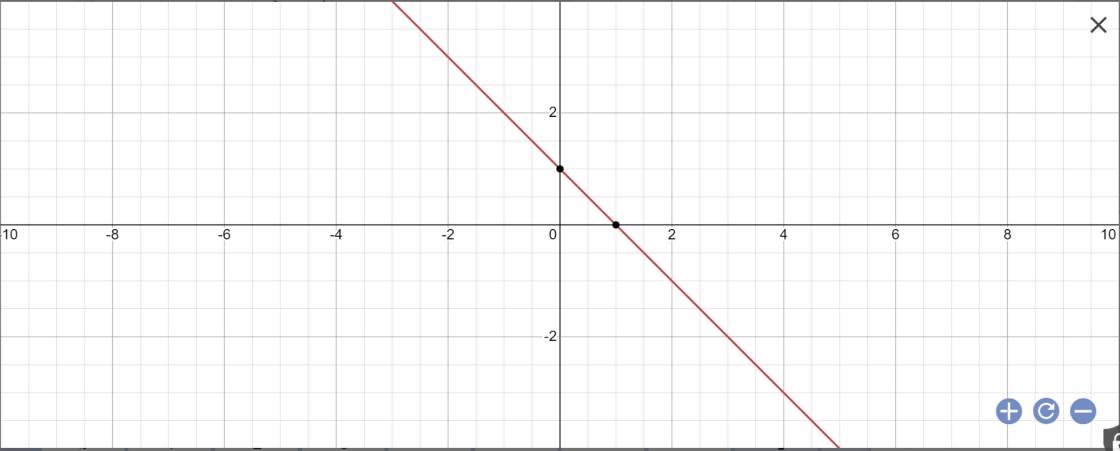
b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox
Ta có: a=-1
nên \(tan\left(180^0-\alpha\right)=-1\)
=>\(180-\alpha=135^0\)
=>\(\alpha=45^0\)
4:
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-8=-x+1\\y=2x-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=9\\y=2x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\cdot3-8=-2\end{matrix}\right.\)
Thay x=3 và y=-2 vào (D), ta được:
\(3\left(m-2\right)+1=-2\)
=>3(m-2)=-3
=>m-2=-1
=>m=1
5: Để (D) cắt (D') tại một điểm trên trục hoành thì
\(\left\{{}\begin{matrix}m-2< >m^2-2\\-\dfrac{1}{m-2}=\dfrac{-m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2-m\ne0\\\dfrac{1}{m-2}=\dfrac{m}{m^2-2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)\ne0\\m^2-2=m^2-2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\notin\left\{0;1\right\}\\-2m=-2\end{matrix}\right.\)
=>\(m\in\varnothing\)
6: (D): y=(m-2)x+1
=>y=mx-2x+1
Điểm mà (D) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)















