Cho ngũ giác đều ABCDE tâm O. Cạnh AB=100m. Tính OA

Những câu hỏi liên quan
Cho ngũ giác đều ABCDE nội tiếp đường tròn tâm O bán kính R. Tính \(\left|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\right|\).
cho ngũ giác đều abcde tâm o chứng minh vecto oa+ob+oc+od+oe=0
Vì O là tâm của ngũ giác abcde nên O cũng là trọng tâm của ngũ giác nên vecto oa+ob+oc+od+oe=0
Đúng 0
Bình luận (0)
1) Cho tam giác ABC đều cạnh 5. M là trung điểm BC. I là trung điểm AM. Tính left|overrightarrow{BI}+overrightarrow{CI}right|2) Cho tam giác ABC đều cạnh 7. G là trọng tâm. M là trung điểm AB. Tính left|overrightarrow{AG}+overrightarrow{AM}right|3) Cho ngũ giác đều ABCDE nội tiếp (O). Tính overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}+overrightarrow{OD}+overrightarrow{OE}
Đọc tiếp
1) Cho tam giác ABC đều cạnh 5. M là trung điểm BC. I là trung điểm AM. Tính \(\left|\overrightarrow{BI}+\overrightarrow{CI}\right|\)
2) Cho tam giác ABC đều cạnh 7. G là trọng tâm. M là trung điểm AB. Tính \(\left|\overrightarrow{AG}+\overrightarrow{AM}\right|\)
3) Cho ngũ giác đều ABCDE nội tiếp (O). Tính \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\)
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai? A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các định của ngũ giác. B. Có 5 vectơ gốc O có độ dài bằng nhau. C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác. D. Các vectơ khác
0
→
có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau.
Đọc tiếp
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
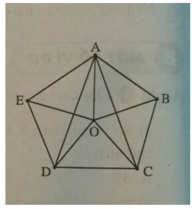
A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các định của ngũ giác.
B. Có 5 vectơ gốc O có độ dài bằng nhau.
C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác.
D. Các vectơ khác 0 → có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau.
Có 5 vectơ mà điểm đầu là O, điểm cuối là đỉnh của ngũ giác: O A → , O B → , O C → , O D → , O E → . Các vectơ này có độ dài bằng nhau (tính chất của các đa giác đều).
Các vectơ khác 0 → có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau, bằng cạnh của ngũ giác đều. Vậy các phương án A, B, D đều đúng, phương án C sai.
Chọn C.
Đúng 0
Bình luận (0)
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O). Tính số đo cung AB
A. 72 °
B. 60 °
C. 120 °
D. 90 °
Chọn đáp án A.
Do ABCDE là ngũ giác đều nội tiếp đường tròn (O) nên:
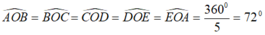
Suy ra, sđ A B ⏜ = 72 °
Đúng 0
Bình luận (0)
cho ngũ giác đều ABCDE đường phân giác góc A,B cắt nhau tại O, M là trung điểm của AB, OM=r, tính diện tích ngũ giác ABCDE
cho ngũ giác đều ABCDE đường phân giác góc A,góc B cắt nhau ở O, M là trung điểm của AB, OM=r,tính diện tích ngũ giác
cho ngũ giác đều ABCDE tâm O. Chứng minh rằng vectoOA+vectoOB+vectoOC+vectoOD+vectoOE=vecto0
Gọi H là trung điểm của CD, do tính chất của ngũ giác đều ta có O nằm trên AH mặt khác AH cũng đi qua trung điểm của BE, ta có:
\(\overrightarrow{OA}\) cùng phương với vtAH
(\(\overrightarrow{OB}+\overrightarrow{OE}\)) là 1 vecto cùng phương với \(\overrightarrow{AH}\)
(\(\overrightarrow{OC}+\overrightarrow{OD}\)) là 1 vecto cùng phương với \(\overrightarrow{AH}\)
=>\(\overrightarrow{V}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\) là vecto cùgn phương với \(\overrightarrow{AH}\)
* Gọi K là trung điểm DE, có BK đi qua O và các trung điểm của AC và DE
\(\overrightarrow{OB}\) cùng phương vớI \(\overrightarrow{BK}\)
\(\overrightarrow{OA}+\overrightarrow{OC}\) : cùng phương với\(\overrightarrow{BK}\)
\(\overrightarrow{OD}+\overrightarrow{OE}\) : cùng phương với \(\overrightarrow{BK}\)
=> \(\overrightarrow{V}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\) là vecto cùng phương với \(\overrightarrow{BK}\)
\(\overrightarrow{AH}\)và \(\overrightarrow{BK}\)là 2 vecto không cùng phương, mà chúng đều cùng phương với \(\overrightarrow{V}\)
nên vtv phải là\(\overrightarrow{0}\) (chỉ có vt0 là vecto cùng phương với 2 vecto không cùng phương)
=>đpcm
Đúng 0
Bình luận (1)
Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
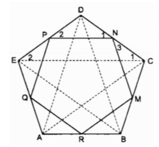
Xét △ ABC và △ BCD:
AB = BC (gt)
∠ B = ∠ C (gt)
BC = CD (gt)
Do đó: △ ABC = △ BCD (c.g.c)
⇒ AC = BD (1)
Xét △ BCD và △ CDE:
BC = CD (gt)
∠ C = ∠ D (gt)
CD = DE (gt)
Do đó: △ BCD = △ CDE (c.g.c) ⇒ BD = CE (2)
Xét △ CDE và △ DEA:
CD = DE (gt)
∠ D = ∠ E (gt)
DE = EA (gt)
Do đó: △ CDE = △ DEA (c.g.c) ⇒ CE = DA (3)
Xét △ DEA và △ EAB:
DE = EA (gt)
∠ E = ∠ A (gt)
EA = AB (gt)
Do đó: △ DEA = △ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong △ ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong △ CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong △ DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong △ EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ((5-2 ). 180 0 )/5 = 108 0
△ DPN cân tại D
⇒ ∠ (DPN) = ∠ (DNP) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
△ CNM cân tại C
⇒ ∠ (CNM) = ∠ (CMN) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (ADN) + ∠ (PNM) + ∠ (CNM) = 180 0
⇒ ∠ (PNM) = 180 0 - ( ∠ (ADN) + ∠ (CNM) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ BMR cân tại B
⇒ ∠ (BMR) = ∠ (BRM) = ( 180 0 - ∠ B )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (CMN) + ∠ (BRM) + ∠ (BMR) = 180 0
⇒ ∠ (NMR) = 180 0 - ( ∠ (CMN) + ∠ (BMR) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ ARQ cân tại A
⇒ ∠ (ARQ) = ∠ (AQR) = ( 180 0 - ∠ A )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (BRM) + ∠ (MRQ) + ∠ (ARQ) = 180 0
⇒ ∠ (MRQ) = 180 0 - ( ∠ (BRM) + ∠ (ARQ) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ QEP cân tại E
⇒ ∠ (EQP) = ∠ (EPQ) = ( 180 0 - ∠ E )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (AQR) + ∠ (RQP) + ∠ (EQP) = 180 0
⇒ ∠ (RQP) = 180 0 - ( ∠ (AQR) + ∠ (EQP) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
∠ (EQP) + ∠ (QPN) + ∠ (DPN) = 180 0
⇒ ∠ (QPN) = 180 0 - ( ∠ (EPQ) + ∠ (DPN) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
Suy ra : ∠ (PNM) = ∠ (NMR) = ∠ (MRQ) = ∠ (RQP) = ∠ (QPN)
Vậy MNPQR là ngũ giác đều.
Đúng 0
Bình luận (0)
Cho ngũ giác đều ABCDE , AB=a Đường phân giác góc A góc B cắt nhau tại O . gọi M là trung điểm của AB , OM=r Tính diện tích ABCDE theo a, theo r














