Gọi M là trung điểm của AB
=>AM=BM=50m và OM vuông góc AB và góc MOA=36 độ
sin AOM=AM/OA
=>50/AO=sin36
=>AO=85,07(m)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
cho ngũ giác đều abcde tâm o chứng minh vecto oa+ob+oc+od+oe=0
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai? A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các định của ngũ giác. B. Có 5 vectơ gốc O có độ dài bằng nhau. C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác. D. Các vectơ khác
0
→
có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau.
Đọc tiếp
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
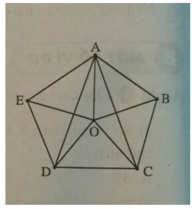
A. Có 5 vectơ mà điểm đầu là O, điểm cuối là các định của ngũ giác.
B. Có 5 vectơ gốc O có độ dài bằng nhau.
C. Có 4 vectơ mà điểm đầu là A, điểm cuối là các đỉnh của ngũ giác.
D. Các vectơ khác 0 → có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau.
Cho ngũ giác ABCDE. Có bao nhiêu vectơ được lập ra từ các cạnh và đường chéo của ngũ giác?
A. 5
B. 10
C. 15
D. 20
Cho hình ngũ giác đều ABCDE (các đỉnh lấy theo thứ tự đó và thuận chiều quay của kim đồng hồ) nội tiếp trong đường tròn lượng giác. Số đo bằng radian của các cung lượng giác AB, DA, FA lần lượt là
Cho ngũ giác ABCDE. Dựng điểm M thỏa mãn điều kiện
M
A
→
+
M
B
→
+
M
C
→
+
M
D
→
+
M
E
→
0
→...
Đọc tiếp
Cho ngũ giác ABCDE. Dựng điểm M thỏa mãn điều kiện M A → + M B → + M C → + M D → + M E → = 0 → . Gọi G là trọng tâm tam giác ABC, H là trung điểm của DE. Khi đó:
A. M là trung điểm của GH
B. M là điểm thỏa mãn MH = 2MG
C. M là điểm thỏa mãn M H → = 3 2 M G →
D. M là điểm thỏa mãn M H → = 3 2 M G →
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).a/ Tìm tọa độ trọng tâm G của tam giác ABC.b/ Tìm tọa độ điểm D để ABCD là hình bình hànhc/ Tìm tọa độ sao cho Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng:
Đọc tiếp
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ 
sao cho 
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ O→ và cùng phương với vectơ OA→.
b) Tìm các vectơ bằng vectơ AB→.
Cho ngũ giác ABCDE từ đỉnh của ngũ giác đã cho có thể lập được bao nhiêu vectơ có điểm cuối là A
Cho hình chữ nhật ABCD tâm O có cạnh AB=2a,OA=a√5.Tính độ dài véc tơ BC
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác O A → và cùng phương với nó là
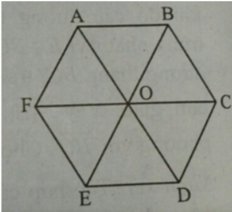
A. 5
B. 6
C. 9
D. 10