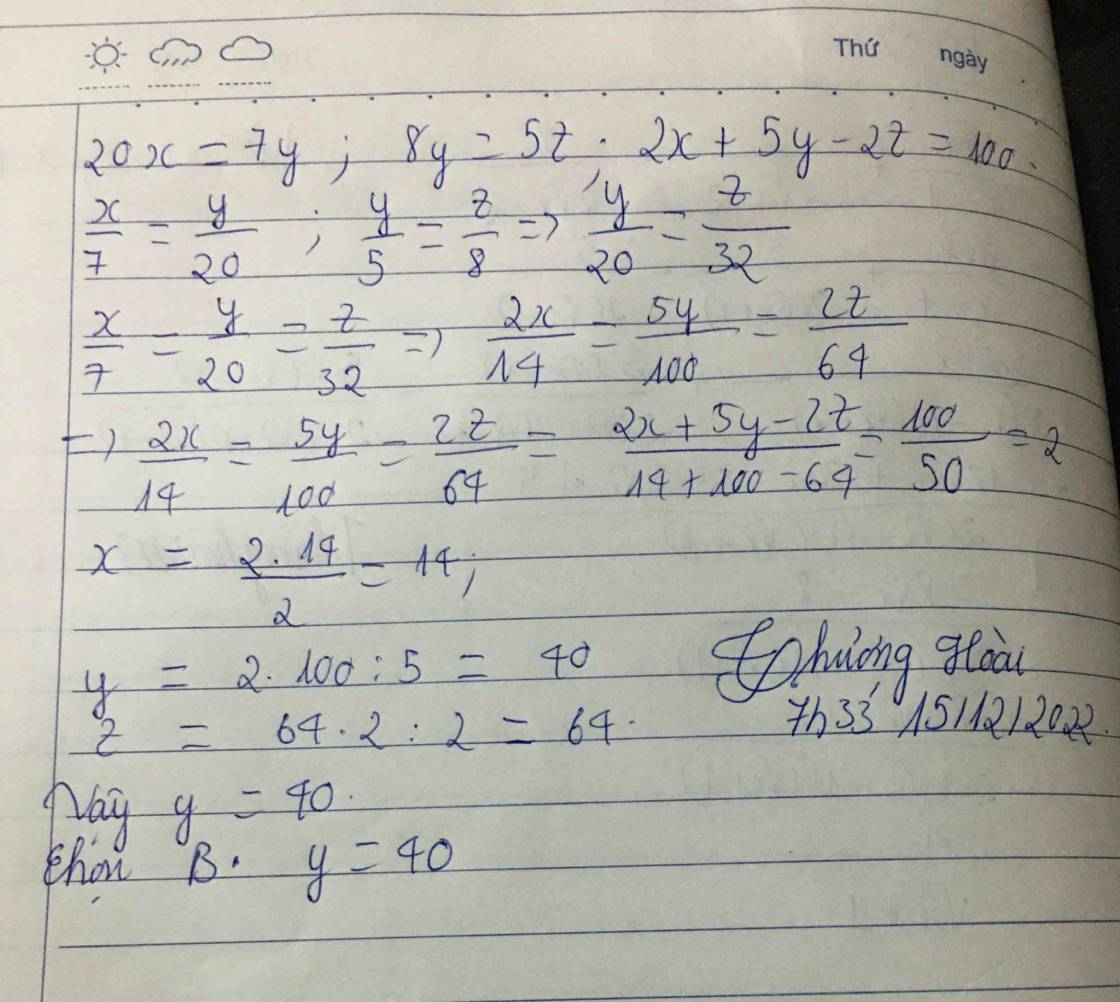cho mk một tk đi bà con ơi

ủng hộ mk đi làm ơn

Bài này hơi rối nhé.

Ta sẽ biến đổi các chữ y;z của biểu thức về x để tính được x => y và z

* 20x = 7y      

 ?x(1)  = 5y 

\(\Rightarrow x\left(1\right)=20:\left(7:5\right)=\frac{100}{7}\)

* 8y = 5z 

Mà: 20x = 7y

        ? x = 8y

=> x = 20 x ( 8 : 7 ) = 160/7

Có: 160/7x = 5z

          ? x(2)    = 2z

\(\Rightarrow x\left(2\right)=\frac{160}{7}:\left(5:2\right)=\frac{64}{7}\)

Thay hết x vừa tìm được vào biểu thức đề cho có (Có kí hiệu số thứ tự x cho dễ nhé)

\(2x+5y-2z=100\)

\(\Leftrightarrow2x+\frac{100}{7}x-\frac{64}{7}x=100\)

\(\Leftrightarrow\frac{50}{7}x=100\)

\(\Leftrightarrow x=100:\frac{50}{7}=14\)

\(\Rightarrow y=20.14:7=40\)

\(\Rightarrow z=40.8:5=64\)

Bài này ko rối, quan trọng là quên cơ bản

Từ \(20x=7y\Rightarrow\frac{x}{7}=\frac{y}{20}\Rightarrow\frac{x}{35}=\frac{y}{100}\left(1\right)\)

\(8y=5z\Rightarrow\frac{y}{5}=\frac{z}{8}\Rightarrow\frac{y}{100}=\frac{z}{160}\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow\frac{x}{35}=\frac{y}{100}=\frac{z}{160}\Rightarrow\frac{2x}{70}=\frac{5y}{500}=\frac{2z}{320}\)

Áp dụng t/c dãy tỉ số bằng nhau ta có: 

\(\frac{2x}{70}=\frac{5y}{500}=\frac{2z}{320}=\frac{2x+5y-2z}{70+500-320}=\frac{100}{250}=\frac{2}{5}\)

\(\Rightarrow\hept{\begin{cases}\frac{x}{35}=\frac{2}{5}\Rightarrow x=\frac{2\cdot35}{5}=14\\\frac{y}{100}=\frac{2}{5}\Rightarrow y=\frac{2\cdot100}{5}=40\\\frac{z}{160}=\frac{2}{5}\Rightarrow z=\frac{2\cdot160}{5}=64\end{cases}}\)

\(x^3+8y^3\\ =x^3+\left(2y\right)^3\\ =\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)

\(8y^3-125\\ =\left(2y\right)^3-5^3\\ =\left(2y-5\right)\left(4y^2+10y+25\right)\)

\(a^6-b^3\\ =\left(a^2\right)^3-b^3\\ =\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)

\(8x^3-\frac{1}{8}\\ =\left(2x\right)^3-\left(\frac{1}{2}\right)^3\\ =\left(2x-\frac{1}{2}\right)\left(4x^2+x+\frac{1}{4}\right)\)

\(x^{32}-1\\ =\left(x^{16}\right)^2-1^2\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)

\(4x^2+4x+1\\ =\left(2x+1\right)^2\)

\(x^2-20x+100\\ =\left(x-10\right)^2\)

\(y^4-14y^2+49\\ =\left(y^2-7\right)^2\)

a/ Ta có:

\(A=x^2-6x+11\)

\(A=x\cdot x-3x-3x+3\cdot3+2\)

\(A=x\left(x-3\right)-3\left(x-3\right)+2\)

\(A=\left(x-3\right)\left(x-3\right)+2\)

\(A=\left(x-3\right)^2+2\)

Vì \(\left(x-3\right)^2\ge0\)

Nên GTNN của \(\left(x-3\right)^2\)là 0

=> \(A_{min}=0+2=2\)

mình chỉ biết a. thôi

a) ta có : \(A=x^2-6x+11\)

\(A=x.x-3x-3x+3.3+2\)

\(A=x\left(x-3\right)-3\left(x-3\right)+2\)

\(A=\left(x-3\right)\left(x-3\right)+2\)

\(A=\left(x-3\right)^2+2\)

vì \(\left(x-3\right)^2\ge0\)

nên GTNN của \(\left(x-3\right)^2\)là \(0\)

\(\Rightarrow\)\(A_{min}\)\(=0+2=2\)

oOo Không đủ can đảm để oOo copy mà nói nhưu mk tự làm

a) \(A=x^2+6x+11\)

\(A=x^2+6x+9+2\)

\(A=\left(x+3\right)^2+2\)

Có: \(\left(x+3\right)^2\ge0\Rightarrow\left(x+3\right)^2+2\ge2\)

Dấu = xảy ra khi: \(\left(x+3\right)^2=0\Rightarrow x+3=0\Rightarrow x=-3\)

Vậy: \(Min_A=2\) tại \(x=-3\)

b) \(B=4x-x^2+1\)

\(B=-x^2+4x-4+5\)

\(B=-\left(x-2\right)^2+5\)

\(B=5-\left(x-2\right)^2\)

Có: \(\left(x-2\right)^2\ge0\)

\(\Rightarrow5-\left(x-2\right)^2\le5\)

Dấu = xảy ra khi: \(\left(x-2\right)^2=0\Rightarrow x-2=0\Rightarrow x=2\)

Vậy: \(Max_B=5\) tại \(x=2\)

d, (x-1) (x+2) (x+3) (x+6)
=(x^2+2x-x-2) (x^2+6x+3x+18)
=(x^2-x^2) + (2x-x+6x-3x) = (-2+18)
=0            + (-8x)              =16
=                    x                =16:(-8)
=                  x                  =-2

A = x^2 + 6x + 11

= x^2 + 6x + 9 + 2

= (x + 3)^2 + 2

min = 2

a, A = x^2 + 6x + 11

= x^2 + 6x + 9 + 2

= (x + 3)^2 + 2

làm tiếp

b, x^2 - 20x + 101

= x^2  20x + 100 + 1

= (x - 10)^2 + 1

có (x - 10)^2 > 0 => (x - 10)^2 +  > 1

a) x²+20x+100=x²+2.10.x+10²

=(x+10)²

Tại x=-100 => ...........

(bn thay vào rồi tự tính nhá)

b) 16y²-8y+1=(4y)²-2.4y+1²

=(4y-1)²

Với y=\(\frac{81}{4}\)=> ............

(bn thay vào rồi tự tính nhá)

c)x³+ 15x²+ 75x+125 =x³+3.x².5+3.x.5²+5³

=(x+5)³

Với x=-25 =>....

d)x³-9x²+27x-27(đề sai đáng ra là -9x² chứ ko phải -9x nha bn)

=x³-3.x²+3.x.3²-3³

=(x-3)³

Với x=13=> ....

tk mk nha

\(x^2+20x+100\)

\(=x^2+2.x.10+10^2\)

\(=\left(x+10\right)^2\)

\(=\left(-110+10\right)^2\)

\(=\left(-100\right)^2=100^2=10000\)