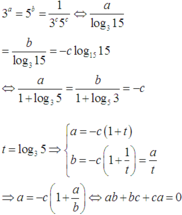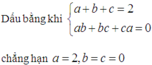cho a,b,c là ba số thực khác 0 thỏa mãn điều kiện a+b-c/c = b+c-a/a = c+a-b/b

Những câu hỏi liên quan
Cho a;b;c là ba số thực dương,
a
1
và thỏa mãn
log
2
a
b
c
+
log
a
b
3
c
3
+
b
c...
Đọc tiếp
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Đúng 0
Bình luận (0)
Cho ba số a, b, c khác nhau và khác 0 thỏa mãn điều kiện: \(\dfrac{a}{b+c}=\dfrac{b}{a+c}=\dfrac{c}{a+b}\) chứng minh rằng \(M=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b}{c}\)
Cho ba số a, b, c khác nhau và khác 0 thỏa mãn điều kiện: \(\dfrac{a}{b+c}=\dfrac{b}{a+c}=\dfrac{c}{a+b}\) chứng minh rằng \(M=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b}{c}\)
Cho ba số a, b, c khác nhau và khác 0 thỏa mãn điều kiện: \(\dfrac{a}{b+c}=\dfrac{b}{a+c}=\dfrac{c}{a+b}\) chứng minh rằng \(M=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b}{c}\)
Ta có: \(\dfrac{a}{b+c}=\dfrac{b}{a+c}\Rightarrow\dfrac{b+c}{a}=\dfrac{a+c}{b}\left(1\right)\)
\(\dfrac{c}{a+b}=\dfrac{b}{a+c}\Rightarrow\dfrac{a+b}{c}=\dfrac{a+c}{b}\left(2\right)\)
Từ (1), (2) \(\Rightarrow\dfrac{b+c}{a}=\dfrac{a+b}{c}=\dfrac{a+c}{b}\)
Đúng 1
Bình luận (0)
Cho ba số a, b, c khác nhau và khác 0 thỏa mãn điều kiện: \(\dfrac{a}{b+c}=\dfrac{b}{a+c}=\dfrac{c}{a+b}\) chứng minh rằng \(M=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b}{c}\)
a+b−cc=b+c−aa=c+a−bb
⇒a+b−cc+1=b+c−aa+1=c+a−bb+1
⇒a+bc=b+ca=c+ab
+)Nếu a+b+c=0⇒a+b=−c;b+c=−a;c+a=−b
⇒B=a+ba.c+ac.b+cb=−ca.−bc.−ab=−(abc)abc=−1
Nếu a+b+c≠0
Áp dụng tính chất dãy tỉ số bằng nhau ta có
a+bc=b+ca=c+ab=2(a+b+c)a+b+c=2
⇒a+b=2c
b+c=2a
c+a=2b
⇒B=2ca.2bc.2ab=2.2.2=8
Đúng 0
Bình luận (0)
. Cho a, b, c là 3 số thực khác 0, thỏa mãn điều kiện: a + b ≠ - c và a b c b c a c a b c a b . Tính giá trị biểu thức: P = 1 1 1 b a c a c b
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a 5b 15-c. Tìm giá trị nhỏ nhất của biểu thức P a2 + b2 + c2 - 4(a+b+c)
Đọc tiếp
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3a = 5b = 15-c. Tìm giá trị nhỏ nhất của biểu thức P = a2 + b2 + c2 - 4(a+b+c)
![]()
![]()
![]()
![]()
Ba số a,b,c khác nhau và khác 0 thỏa mãn điều kiện a/b+c=b/a+c=c/a+b
Tính giá trị biểu thức P=b+c/a + a+c/b + a+b/c
\(\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}\)
cộng 1 vào mỗi tỉ số,ta được :
\(\frac{a}{b+c}+1=\frac{b}{a+c}+1=\frac{c}{a+b}+1\)
\(\frac{a+b+c}{b+c}=\frac{a+b+c}{a+c}=\frac{a+b+c}{a+b}\)
xét a + b + c = 0 \(\Rightarrow\)a + b = -c ; b + c = -a ; a + c = -b
\(\Rightarrow P=\frac{-a}{a}+\frac{-b}{b}+\frac{-c}{c}=\left(-1\right)+\left(-1\right)+\left(-1\right)=-3\)
xét a + b + c khác 0 \(\Rightarrow\)b + c = a + c = a + b \(\Rightarrow\)a = b = c
\(\Rightarrow P=2+2+2=6\)
Đúng 0
Bình luận (0)
Có : a/b+c = b/a+c = c/a+b => b+c/a = a+c/b = a+b/c
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
b+c/a = a+c/b = a+b/c = b+c+a+c+a+b/a+b+c = 2
=> P = 2+ 2 + 2 =6
k mk nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a,b,c là 3 số thực khác 0, thỏa mãn điều kiện:
a+b-c / c = b+c-a /a = c+a-b / b
Hãy tính B = ( 1+b/a).(1+a/c).(1+c/b)
Giải: Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{a+b-c}{c}=\frac{b+c-a}{a}=\frac{c+a-b}{b}=\frac{\left(a+b-c\right)+\left(b+c-a\right)+\left(c+a-b\right)}{c+a+b}=\frac{a+b+c}{a+b+c}=1\) (vì a,b,c \(\ne\)0)
=> \(\hept{\begin{cases}\frac{a+b-c}{c}=1\\\frac{b+c-a}{a}=1\\\frac{c+a-b}{b}=1\end{cases}}\) => \(\hept{\begin{cases}a+b-c=c\\b+c-a=a\\c+a-b=b\end{cases}}\)=> \(\hept{\begin{cases}a+b=2c\\b+c=2a\\c+a=2b\end{cases}}\)
Khi đó, ta có: B = \(\left(1+\frac{b}{a}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{c}{b}\right)\)
B = \(\left(\frac{a+b}{a}\right)\left(\frac{a+c}{c}\right)\left(\frac{b+c}{b}\right)\)
B = \(\frac{2c}{a}.\frac{2b}{c}.\frac{2a}{b}=8\)
Vậy ...
(xem lại đề)
Đúng 0
Bình luận (0)
Cho a,b,c là 3 số thực khác 0, thỏa mãn điều kiện:
a+b-c / c = b+c-a /a = c+a-b / b
Hãy tính B = ( 1+b/a).(1+a/c).(1+c/b)
Đúng 0
Bình luận (0)