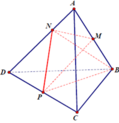
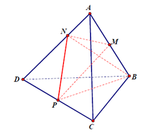
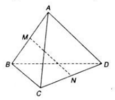
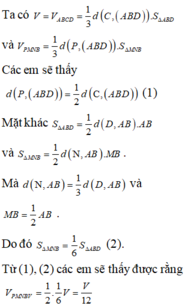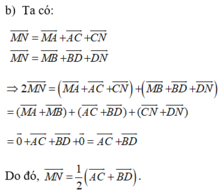cho tứ diện ABCD có M N lần lượt là trung điểm AB , CD ;P thuộc AD và không là trung điểm AD.Tìm thiết diện của chóp và (MNP)

Những câu hỏi liên quan
Cho hình tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện đi qua ba điểm M, N, P là:
A. hình thang
B. hình bình hành
C. hình thoi
D. hình chữ nhật
Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp A.
G
A
→
+
G
B
→
+
G
C
→
+
G
D...
Đọc tiếp
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
A. G A → + G B → + G C → + G D → = 0 →
B. 4 P G → = P A → + P B → + P C → + P D → với P là điểm bất kỳ
C. G M = G N
D. G M → + G N → = 0 →
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp với P là điểm bất kỳ
Đọc tiếp
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
![]()
![]() với P là điểm bất kỳ
với P là điểm bất kỳ
![]()
![]()
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không là trung điểm của BC). Thiết diện của tứ diện bị cắt bởi mặt phẳng M N P là
A. một tứ giác
B. một ngũ giác
C. một lục giác
D. một tam giác
Chọn đáp án A
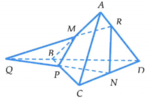
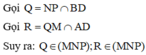
Vậy thiết diện của tứ diện bị cắt bởi mặt phẳng (MNP) là tứ giác MRNP
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho
A
D
3
A
N
. Tính thể tích của tứ diện B.MNP. A.
V
4
B.
V
12
C.
V
8
D.
V
64
Đọc tiếp
Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho A D = 3 A N . Tính thể tích của tứ diện B.MNP.
A. V 4
B. V 12
C. V 8
D. V 64
Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho
A
D
3
A
N
. Tính thể tích của tứ diện BMNP.
A
.
V
4
.
B
.
V
12
.
C
.
V
8
.
D...
Đọc tiếp
Cho tứ diện ABCD có thể tích là V, hai điểm M và P lần lượt là trung điểm của AB, CD; điểm N thuộc AD sao cho A D = 3 A N . Tính thể tích của tứ diện BMNP.
A . V 4 .
B . V 12 .
C . V 8 .
D . V 64 .
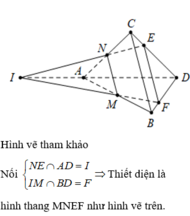
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho
E
D
3
E
C
. Thiết diện tạo bởi mặt phẳng
M
N
E
và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho E D = 3 E C . Thiết diện tạo bởi mặt phẳng M N E và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD
C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC
D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp A. GM GN B.
G
M
→
+
G
N
→
0
→
C.
G
A
→...
Đọc tiếp
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
A. GM = GN
B. G M → + G N → = 0 →
C. G A → + G B → + G C → + G D → = 0
D. P G → = 1 / 4 ( P A → + P B → + P C → + P D → ) , với P là điểm bất kì.
Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD. Gọi M và N lần lượt là các trung điểm của AB và CD.
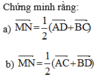
Cho tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây là sai?
A
.
M
N
⊥
A
B
B
.
M
N
⊥
B
D
C
.
M
N
⊥
C
D
D
.
A
B
⊥
C
D
Đọc tiếp
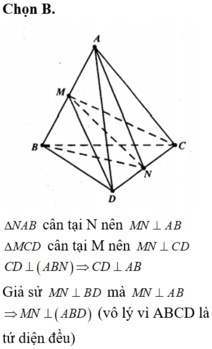
Cho tứ diện đều ABCD có M, N lần lượt là trung điểm của các cạnh AB và CD. Mệnh đề nào sau đây là sai?
A . M N ⊥ A B
B . M N ⊥ B D
C . M N ⊥ C D
D . A B ⊥ C D