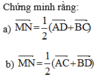Các câu hỏi tương tự
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp A. GM GN B.
G
M
→
+
G
N
→
0
→
C.
G
A
→...
Đọc tiếp
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
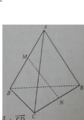
A. GM = GN
B. G M → + G N → = 0 →
C. G A → + G B → + G C → + G D → = 0
D. P G → = 1 / 4 ( P A → + P B → + P C → + P D → ) , với P là điểm bất kì.
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A
B
→
+
A
C
→
+
A
D
→
bằng: A.
4
A
G...
Đọc tiếp
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
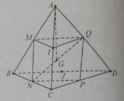
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN và P là một điểm bất kỳ trong không gian. Chứng minh rằng :
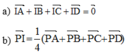
Cho tứ diện ABCD có E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mp (ACD) là
A. điểm F
B. giao điểm của EG và AF
C. Giao điểm của EG và AC
D. giao điểm của EG và CD
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm
∆
BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là: A. điểm C B. điểm N C. giao điểm của đường thẳng MG và đường thẳng AN D. giao điểm của đường thẳng MG và đường thẳng BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm ∆ BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
A. điểm C
B. điểm N
C. giao điểm của đường thẳng MG và đường thẳng AN
D. giao điểm của đường thẳng MG và đường thẳng BC
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành? A. AB3CD B. AB2CD C. CD2AB D. CD3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp 
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
Cho hình tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện đi qua ba điểm M, N, P là:
A. hình thang
B. hình bình hành
C. hình thoi
D. hình chữ nhật
Cho hình tứ diện ABCD. Gọi M và N lần lượt là các trung điểm của AB và CD.
