cho tam giác abc . d là trung điểm của ab . e là trung điểm của cạnh ac.
chứng minh : DE//BC va De =1/2 BC
Những câu hỏi liên quan
cho tam giác ABC D LÀ TRUNG ĐIỂM CỦA CẠNH AB E LÀ TRUNG ĐIỂM CỦA CẠNH AC .CHỨNG minh DE //BC và DE bằng 1/2 BC
cho tam giác abc d là trung điểm của ab e là trung điểm của cạnh ac Chứng minh để // bc và de = 1/2 bc
1 tháng 12 2021 lúc 20:25
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng :
a)BD = CF
b)DE // BC và DE = 1/2 BC
Cho tam giác ABC, D là trung điểm của cạnh AB, E là trung điểm của cạnh AC. Trên tia đối của tia ED lấy điểm F sao cho EF = ED. Chứng minh rằng:
a) CF = BD và CF // AB.
b) DE // BC và BC = 2. DE.
a) Xét ΔAED và ΔCEF có
EA=EC(E là trung điểm của AC)
\(\widehat{AED}=\widehat{CEF}\)(hai góc đối đỉnh)
ED=EF(gt)
Do đó: ΔAED=ΔCEF(c-g-c)
⇒AD=CF(hai cạnh tương ứng)
mà AD=BD(D là trung điểm của AB)
nên CF=BD(đpcm)
Ta có: ΔAED=ΔCEF(Cmt)
nên \(\widehat{ADE}=\widehat{CFE}\)(hai góc tương ứng)
mà \(\widehat{ADE}\) và \(\widehat{CFE}\) là hai góc ở vị trí so le trong
nên AD//CF(Dấu hiệu nhận biết hai đường thẳng song song)
hay CF//AB(đpcm)
Đúng 4
Bình luận (0)
a) Xét ΔAED và ΔCEF có EA=EC(E là trung điểm của AC) ˆ A E D = ˆ C E F (hai góc đối đỉnh) ED=EF(gt) Do đó: ΔAED=ΔCEF(c-g-c) ⇒AD=CF(hai cạnh tương ứng) mà AD=BD(D là trung điểm của AB) nên CF=BD(đpcm) Ta có: ΔAED=ΔCEF(Cmt) nên ˆ A D E = ˆ C F E (hai góc tương ứng) mà ˆ A D E và ˆ C F E là hai góc ở vị trí so le trong nên AD//CF(Dấu hiệu nhận biết hai đường thẳng song song) hay CF//AB(đpcm) a) Xét ΔAED và ΔCEF có EA=EC(E là trung điểm của AC) ˆ A E D = ˆ C E F (hai góc đối đỉnh) ED=EF(gt) Do đó: ΔAED=ΔCEF(c-g-c) ⇒AD=CF(hai cạnh tương ứng) mà AD=BD(D là trung điểm của AB) nên CF=BD(đpcm) Ta có: ΔAED=ΔCEF(Cmt) nên ˆ A D E = ˆ C F E (hai góc tương ứng) mà ˆ A D E và ˆ C F E là hai góc ở vị trí so le trong nên AD//CF(Dấu hiệu nhận biết hai đường thẳng song song) hay CF//AB(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có D là trung điểm của cạnh AB và E là trung điểm của cạnh AC. Trên tia DE lấy điểm F sao cho E là trung điểm của đoạn thẳng DF
a) Chứng minh Tam giác AED=tam giác CEF
b) Chứng minh: AB// CF
c) Chứng minh: DE bằng một nữa của BC
Cho tam giác ABC có trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt AC ở E.1) Chứng minh : DE // BC.2) Gọi G là giao điểm AM với DE. Chứng minh G là trung điểm của DE. Tìm điều kiện của tam giác ABC để G là trung điểm của AM.3) Gọi AN là phân giác của góc BAC, (N thuộc BC). Biết AB 12cm, AC 16cm, BC 20cm. Tính diện tích tam giác AMNgiúp tớ zới ạ:
Đọc tiếp
Cho tam giác ABC có trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt AC ở E.
1) Chứng minh : DE // BC.
2) Gọi G là giao điểm AM với DE. Chứng minh G là trung điểm của DE. Tìm điều kiện của tam giác ABC để G là trung điểm của AM.
3) Gọi AN là phân giác của góc BAC, (N thuộc BC). Biết AB = 12cm, AC = 16cm, BC = 20cm. Tính diện tích tam giác AMN
giúp tớ zới ạ:<
1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ
Đúng 1
Bình luận (1)
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng: DE//BC và DE =1/2BC
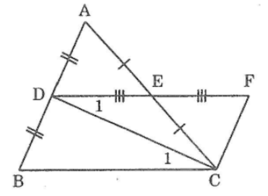
Ta có: ΔBDC= ΔFCD(chứng minh trên)
Suy ra: ∠(C1 ) =∠(D1 ) (hai góc tương ứng)
Suy ra: DE // BC ( vì có hai góc so le trong bằng nhau)
ΔBDC= ΔFCD suy ra BC = DF (hai cạnh tương ứng)
Mà DE = 1/2 DF(gt). Vậy DE = 1/2 BC
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC trên cạnh AB lấy điểm D sao cho AD=2/5AB, trên cạnh AC lấy điểm E sao cho AE=2/5AC a/CM DE//BC b/ đường trung tuyến AI cắt DE tại M. Chứng minh M là trung điểm của DE. c/ đường phân giác của góc BAC cắt BC tại I. Chứng minh IB. AE=IC.AD
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABI có DM//BI
nên DM/BI=AD/AB
Xét ΔACI có EM//IC
nên EM/CI=AE/AC
=>DM/BI=EM/CI
=>DM=EM
=>M là trung điểm của DE
c: AI là phân giác
=>IB/IC=AB/AC=AD/AE
=>IB*AE=IC*AD
Đúng 0
Bình luận (0)
Cho tam giác ABC
a/ Qua D là trung điểm của cạnh AB kẻ DE song song với BC (E thuộc AC) . Chứng minh: EA=EC
b/Nếu D và C lần lượt là trung điểm của AB và AC . Chứng minh: DE song song với BC
Liên Hồng Phúc nó tương tự chứ ko có giống hết 
Đúng 0
Bình luận (0)