cho tam giác MNP, NP= 6 cm, MN= 10 cm, MP= 8 cm
CMR: tam giác MNR vuông
vẽ hình hộ luôn
Cho tam giác MNP vuông tại M (MN<MP). Trên NP lấy Q sao cho NM=NQ. Qua Q, kẻ d vuông góc với NP, d cắt MP tại R.
a)Nếu góc MNP=2MPN. Tính số đo 2 góc đó?
b)CM: Tam giác MNR= tam giác QNR, từ đó suy ra NR là phân giác của góc MNP
c)Trên tia đối của tia MN,lấy K sao cho MK=MN.
CM: Tam giác PNK cân
Cho tam giác MNP vuông tại M (MN<MP). Trên NP lấy Q sao cho NM=NQ. Qua Q, kẻ d vuông góc với NP, d cắt MP tại R.
a)Nếu góc MNP=2MPN. Tính số đo 2 góc đó?
b)CM: Tam giác MNR= tam giác QNR, từ đó suy ra NR là phân giác của góc MNP
c)Trên tia đối của tia MN,lấy K sao cho MK=MN.
CM: Tam giác PNK cân
Cho tam giác MNP vuông ở M, MN = 6 cm, MP = 8 cm. Vẽ hình. a,Tính NP,N;P. b, Phân giác của góc M cắt NP tại E. Tính NE, PE.
a: NP=10(cm)
\(\widehat{P}=37^0\)
\(\widehat{N}=53^0\)
a, \(NP=\sqrt{MN^2+MP^2}=10\left(cm\right)\)
\(\sin N=\dfrac{MP}{NP}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{N}\approx53^0\\ \widehat{P}=90^0-\widehat{N}\approx37^0\)
b, \(\dfrac{NE}{PE}=\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow NE=\dfrac{3}{4}PE\)
\(NE+PE=NP=10\Rightarrow\dfrac{7}{4}PE=10\Rightarrow\left\{{}\begin{matrix}PE=\dfrac{40}{7}\left(cm\right)\\NE=\dfrac{30}{7}\left(cm\right)\end{matrix}\right.\)
Đề bài 1:Cho tam giác ABC cân tại A biết A = 80* . Tính số đo của góc B và C
Để bài 2 :Cho tam giác MNP có MN = 6 cm , MP = 8 cm , NP = 10 cm . Chứng minh tam giác MNP vuông
đề 2 :
MN = 6 cm, MP= 8 cm , NP= 10 cm
ta có : mn^2 + mp^2=6^2+8^2=100
np^2=100
suy ra mp^2+mn^2=np^2
vậy tam giác mnp vuông tại M
kick mk nha
đề 1: vì tổng 3 góc trong 1 tam giác là 180*
mà tam giác abc cân tại a suy ra : góc b = góc c
góc b +góc c=180-80=100
vì góc b = góc c suy ra :
góc b = góc c = 50 *
1/ Ta có \(\widehat{B}+\widehat{C}=180^o-\widehat{A}\) (tổng 3 góc trong của tam giác)
và \(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
=> \(2\widehat{B}=180^o-\widehat{A}\)
=> \(\widehat{B}=\frac{180^o-\widehat{A}}{2}\)
=> \(\widehat{B}=\frac{180^o-80^o}{2}\)
=> \(\widehat{B}=\widehat{C}=\frac{100^o}{2}=50^o\)
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
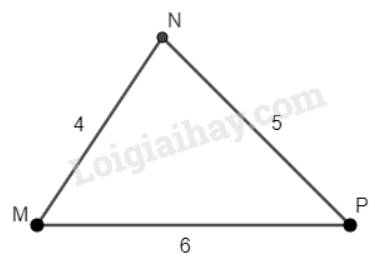
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
Cho tam giác MNP vuông tại M (MN<MP). Vẽ đường cao MH(H thuộc NP)
a. Chứng minh tam giác MNP đồng dạng với tam giác HNM
b. Chứng minh MN^2=NH.NP
c. Vẽ tia phân giác MK của góc NMP (K thuộc NP). Biết MN=7,2 cm và MP=9,6 cm. Tính độ dài các đoạn thẳng NP, NH và MK.
tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)
Mình nghĩ MK nên áp dụng ta lét nhé
7,2/x = 12/9,6-x
<=>7,2 . (9.6-x) = 12.x
<=>69,12 - 7,2x = 12x
<=>69,12 = 12x + 7,2x
<=> 69,12 = 19, 2
<=> x = 69,12 : 19,2 = 3,6
Vậy MK bằng 3,6cm
(mình ko chắc đúng ko nhưng theo mình là vậy)
cho tam giác MNP vuông tại M có MN = 6 cm,MP=8 cm .khi đó NP bằng
A. 100cm B.10cm C.14cm D.48cm
cho tam giác MNP có MN < MP . Kẻ tia phân giác MK của NMP ( K thuộc NP ) . Trên cạnh MP lấy điểm E sao cho ME = MN , trên tia MN lấy điểm F sao cho MF = MP
a) Cm Tam giác NMK = Tam giác EMK
b) Cm KF = KP
c) Cm Tam giác FKN = Tam giác PKE
d) CM ba điểm F ; K ; E thẳng hàng
a: Xét ΔMNK và ΔMEK có
MN=ME
góc NMK=góc EMK
MK chung
=>ΔMNK=ΔMEK
b,c: Xét ΔKNF và ΔKEP có
KN=KE
góc KNF=góc KEP
NF=EP
=>ΔKNF=ΔKEP
=>KF=KP
d: ΔKNF=ΔKEP
=>góc NKF=góc EKP
=>góc EKP+góc PKF=180 độ
=>F,K,E thẳng hàng