Cho tam giác ABC có góc B= góc C
CMR AB=AC
Ko giải theo cách tam giác cân
Những câu hỏi liên quan
cho tam giác ABC cân tại A. đường phân giác AM. biết AB=5cm,BC=6cm
a.CMR: tam giác AMB=tam giác AMC
b. tính AM
C.vì MH vuông góc với AB, MK vuông góc với AC
và MH cắt AC tại P, MK cắt AB tại C
CMR: tam giác MQP cân'giúp với mik đg cần gấp
a: Xét ΔAMB và ΔAMC có
AB=AC
góc BAM=góc CAM
AM chung
=>ΔAMB=ΔACM
b:
ΔABC cân tại A có AM là phân giác
nên AM vuông góc BC và M là trung điểm của BC
MB=MC=BC/2=3cm
=>AM =căn 5^2-3^2=4cm
c: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
góc B=góc C
=>ΔMHB=ΔMKC
=>MH=MK
Xét ΔHMQ vuông tại H và ΔKMP vuôg tại K có
MH=MK
góc HMQ=góc KMP
=>ΔHMQ=ΔKMP
=>MQ=MP
=>ΔMQP cân tại M
Đúng 0
Bình luận (0)
Cho tam giác ABC. Tia phân giác góc ABC cắt cạnh AC tại D. Tia phân giác goác ACB cắt AB tại E. Biết góc BDE=18 độ và góc CED=24 độ. Tính số đo mỗi góc tam giác ABC (Giải cách thông thường đừng giải cách nâng cao như tam giác cân , chương III của môn toán lớp 7 )
Cho tam giác ABC có AH vuông góc vs BC và BAH= 2C . Tia phân giác của góc B cắt AC ở E
a, tia phân giác của góc BAH cắt BE ở I. CMR : tam giác AIE vuông cân
b, CMR: HE là tia phân giác của góc AHC
Có hình và giải theo cách lớp 7 nhé
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB BC 2a. Tam giác SAC cân tại S có đường cao và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a.
A
.
a
3
3
B
.
2
a
3
C
.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a.
A . a 3 3
B . 2 a 3
C . a 3 2
D . a
Đáp án A.
Theo giả thiết ta có SO ⊥ (ABC). Gọi D là điểm đối xưng với B qua O
=> ABCD là hình vuông => AB//CD
=> d(AB;SC) = d(AB;(SCD)) = d(E;(SCD)) = 2d(O;(SCD))(Với E, F lần lượt là trung điểm của AB và CD).
Áp dung tính chất tứ diện vuông cho tứ diện OSCD ta có:
Đúng 0
Bình luận (0)
Cho 2 tam giác ABC và tam giác ACD. Biết tam giác ABC cân tại A, AB=8cm, CD=6cm, góc BAC=35 độ, góc CAD=43 độ. Tính BC, góc ADC, khoảng cách từ B đến AD
Xem chi tiết
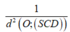
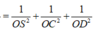
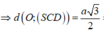
Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(cos35=\dfrac{8^2+8^2-BC^2}{2\cdot8\cdot8}\)
=>\(128-BC^2=2\cdot64\cdot cos35=128\cdot cos35\)
=>\(BC=\sqrt{128-128\cdot cos35}\simeq4,81\left(cm\right)\)
Xét ΔADC có \(\dfrac{CD}{sinCAD}=\dfrac{AC}{sinADC}\)
=>\(\dfrac{8}{sinADC}=\dfrac{6}{sin43}\)
=>\(sinADC=8\cdot\dfrac{sin43}{6}\simeq0,91\)
=>\(\widehat{ADC}\simeq65^0\)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại B, có góc B = 400 ,BA = 3 cm.hãy nêu cách vẽ tam giác cân ABC và tính hai cạnh BC và cạnh AC?
2) Cho tam giác ABC cân tại C .CA = CB = 10 cm. AB = 12 cm.kẻ CI vuông góc với AB
a) chững minh IA = IB
b) Tính IC
cho tam giác abc vuông tại a có đường cao ah.Các tia phân của các góc ACD và DCB cắt cạnh huyền AB theo thứ tự ở K và M. a) cm tam giác ACM cân b) CM điểm cách đều 3 đỉnh của tam giác KCM thì cũng cách đều 3 cạnh của tam giác ABC
Cho tam giác ABC có AB=BC=CA. Tính các góc của tam giác ABC
(làm theo tam giác cân giúp mk nha, mk cần gấp)
Vì \(AB=BC\) nên \(\widehat{C}=\widehat{A}\)
Vì \(BC=CA\) nên \(\widehat{A}=\widehat{B}\)
\(\Rightarrow\) \(\widehat{A}=\widehat{B}=\widehat{C}\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\) \(180^0:3\) \(=60^0\)
Vậy các góc của \(\Delta ABC\) đều có số đo là \(60^0\)
Đúng 1
Bình luận (0)
cho tam giác ABC có góc B=C.Tia phân giác của góc A cắt BC tại D. Chứng minh rằng:
a.ADB=ADC
b.tam giác ADB= tam giác ADC
c. AB=AC
(có vẽ hình)
LƯU Ý: giải theo góc- cạnh- góc