Cho đường tròn (O) bán kính OA4cm Dây BC vuông góc vói OA tại trung điểm của OA Tính độ dài BC

Những câu hỏi liên quan
Cho đường tròn tâm (O) có bán kính OA= 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm OA. Tính độ dài dây BC
3 căn 3/5 nhé
nếu cần trình bày thì bn kẻ hình ra
rồi có ob=oa=oc
ad đl pytago cho tam giác vuoong nnhes
Đúng 0
Bình luận (0)
Cho đường tròn (O) bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
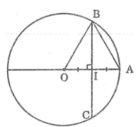
Gọi I là trung điểm của AB
Suy ra: IO = IA = (1/2).OA = 3/2
Ta có: BC ⊥ OA (gt)
Suy ra: góc (OIB) = 90 °
Áp dụng định lí Pitago vào tam giác vuông OBI ta có: O B 2 = B I 2 + I O 2
Suy ra: B I 2 = O B 2 - I O 2
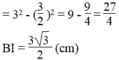
Ta có: BI = CI (đường kính dây cung)
![]()
Đúng 1
Bình luận (0)
- Gọi I là giao điểm của BC và OC
( IO = IA = 1,5cm ) ( OB = OA = 3cm )
Áp dụng đlí Py - ta - go cho tam giác vuông IBO ( ^I = 90^o ) , ta có :
\(OB^2=IB^2+IO^2\)
\(3^2=IB^2+1,5^2\)
\(IB^2=3^2-1,5^2=9-2,25=6,75\)
\(\Rightarrow IB=\sqrt{6,75}\approx2,6\)
Mà \(OA\perp BC\Rightarrow IC=IB\)( t/c đường kính vuông với dây cung )
=> BC = 2 . IB = 2 . 2,6 = 5,2
Vậy : BC = 5,2cm
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC ?
Ta có BC ⊥ OA ⇒ BE = EC
E là trung điểm của OA ⇒ OE = AE và OA=OB= 3cm
OE=\(\dfrac{OA}{2}\) =\(\dfrac{3}{2}\) = 1.5 cm
ΔHBO vuông tại E :
BE=\(\sqrt{OB^2-OE^2}\)
=\(\sqrt{3^2-1.5^2}\) =\(\dfrac{3\sqrt{3}}{2}\) cm
⇒ BC= 2BE
= 2. \(\dfrac{3\sqrt{3}}{2}\) = \(3\sqrt{3}\) cm
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có bán kính OA R, dây BC vuông góc vói OA tại trung điểm M của OAa, Tứ giác OCAB là hình gì? Vì sao?b, Kẻ tiếp tuyến với đường tròn tại B, cắt đường thẳng OA tại E. Tính độ dài BE theo R
Đọc tiếp
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc vói OA tại trung điểm M của OA
a, Tứ giác OCAB là hình gì? Vì sao?
b, Kẻ tiếp tuyến với đường tròn tại B, cắt đường thẳng OA tại E. Tính độ dài BE theo R
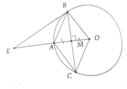
a, OA vuông góc với BC tại M
=> M là trung điểm của BC
=> OCAB là hình thoi
b, Tính được BE = R 3
Đúng 0
Bình luận (0)
Cho đường tròn ( O ) bán kính
O A = 12 c m . Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Độ dài BC là
Bài 2: Cho đường tròn (O) bán kính OA=6cm. Dây BC của đường tròn vuông góc với OA tại trung điểm I của OA
a) C/m tam giác OAB đều
b) Tính độ dài BC
a: Xét (O) có
OI là một phần đường kính
BC là dây
OI\(\perp\)BC tại I
Do đó: I là trung điểm của BC
Xét tứ giác OBAC có
I là trung điểm của BC
I là trung điểm của OA
Do đó: OBAC là hình bình hành
mà OB=OC
nên OBAC là hình thoi
Xét ΔOAB có OA=OB=BA
nên ΔOAB đều
Đúng 0
Bình luận (0)
Bài 2: Cho đường tròn (O) bán kính OA=6cm. Dây BC của đường tròn vuông góc với OA tại trung điểm I của OA
a) C/m tam giác OAB đều
b) Tính độ dài BC
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều => ∠AOB = 60o
Trong tam giác OBE vuông tại B ta có:
BE = OB.tg∠AOB = OB.tg60o = R.√3
Đúng 0
Bình luận (0)
Cho đường tròn (O) có bán kính OA 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính BC. A.
B
C
3
3
c
m
B.
B
C
2
3
c
m
C.
B
C
3
2
c
m
D.
B
C
3...
Đọc tiếp
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính BC.
A. B C = 3 3 c m
B. B C = 2 3 c m
C. B C = 3 2 c m
D. B C = 3 2 2 c m
Đáp án A
Gọi H là trung điểm của BC.
Do dây BC vuông góc với OA tại H nên ta có:
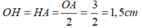
Áp dụng định lí Pytgo vào tam giác OHB vuông tại H ta có:
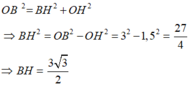
Theo định lí quan hệ vuông góc đường kính và dây ta có: H là trung điểm BC nên:
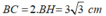
Đúng 0
Bình luận (0)
Cho (O) bán kính 3cm. Dây BC vuông góc OA tại trung điểm của OA. Tính độ dài BC.
Lời giải:
Gọi $K$ là trung điểm $AO$ thì $OK=AO:2=3:2=1,5$ (cm)
Xét tam giác vuông $BKO$ vuông tại $K$,áp dụng định lý Pitago:
$BK=\sqrt{BO^2-OK^2}=\sqrt{3^2-1,5^2}=\frac{3\sqrt{3}}{2}$
Vì dây $BC\perp OA$ tại $K$ nên $K$ là trung điểm của $BC$
$\Rightarrow BC=2BK=3\sqrt{3}$ (cm)
Đúng 1
Bình luận (0)



















