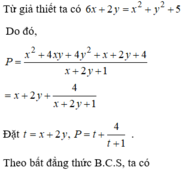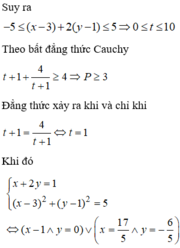cho các số thực dương x , y thỏa mãn 7x^2 - 13xy - 2y^2 = 0

Những câu hỏi liên quan
Cho các số dương x, y thỏa mãn: \(7x^2-13xy-2y^2=0\). Tính \(A=\frac{2x-6y}{7x+4y}\).
cho x,y>0 thỏa mãn \(7x^2-13xy-2y^2=0\)
tính \(A=\frac{2x-6y}{7x+4y}\)
\(7x^2-13xy-2y^2=0\)
\(\Leftrightarrow7x^2-14xy+xy-2y^2=0\)
\(\Leftrightarrow7x\left(x-2y\right)+y\left(x-2y\right)=0\)
\(\Leftrightarrow\left(7x+y\right)\left(x-2y\right)=0\)
\(\Leftrightarrow x=2y\) (do x;y>0)
Do đó: \(A=\frac{2.2y-6y}{7.2y+4y}=\frac{-2y}{18y}=-\frac{1}{9}\)
Cho x,y là hai số thực thỏa mãn x+y=0 . Tính giá trị biểu thức :
\(M=4x-20x^2y+7x^2y^3+2018-20xy^2+4y+7x^3y^2\)
cho x,y là các số thực dương thỏa mãn (x+2019)-y^2=căn(y+2019)-x^2. Tìm Amin=x^2+2xy-2y^2+2y+2019
\(\sqrt{x+2009}-y^2=\sqrt{y+2009}-x^2\)
<=> \(\left(\sqrt{x+2009}-\sqrt{y+2009}\right)+\left(x^2-y^2\right)=0\)
<=> \(\left(x-y\right)\left(\frac{1}{\sqrt{x+2009}+\sqrt{y+2009}}+x+y\right)=0\)
<=> x - y = 0 vì x; y dương
<=> x = y
khi đó: \(A=x^2+2x^2-2x^2+2x+2009=x^2+2x+2009\)
Bạn xem lại đề nhé!
Cho số thực x, y thỏa mãn hệ thức: x^2+2xy+7x+7y+2y^2+10=0. Hãy tìm giá tri lớn nhất, nhỏ nhất của: S=x+y+1.
Cho hai số thực dương x, y thỏa mãn điều kiện
3
+
ln
x
+
y
+
1
3
x
y
9
x
y
−
3
x
−
3
y
....
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn điều kiện 3 + ln x + y + 1 3 x y = 9 x y − 3 x − 3 y . Giá trị nhỏ nhất của biểu thức P = x.y là:
A. 1 9
B. 1 3
C. 1
D. 9
Đáp án C.
Từ giả thiết ta có
ln x + y + 1 + 3 x + y + 1 = ln 3 x y + 3.3 x y (*)
Xét f t = ln t + 3 t hàm trên 0 ; + ∞ , ta có f ' t = 1 t + 3 > , ∀ t > 0
Do đó * ⇔ x + y + 1 = 3 x y ⇔ 3 x y − 1 = x + y ≥ 2 x y ⇔ 3 xy − 2 x y − 1 ≥ 0
Suy ra x y ≥ 1 ⇒ x y ≥ 1.
Đúng 0
Bình luận (0)
Câu 1 cho x,y>0 thỏa mãn xy=6 tìm min Q=2/x+3/y+6/3x+2y
Câu 2 cho x,y là các số thực dương thỏa mãn x+y<=1 tìm min P=(1/x+1/y)nhân với căn (1+x^2y^2)
Bạn nào giúp mình nhanh với mình đang cần gấp T.T
Cho x, y là các số thực thỏa mãn
(
x
−
3
)
2
+
(
y
−
1
)
2
5
. Giá trị nhỏ nhất của biểu thức
P
3
y
2
+...
Đọc tiếp
Cho x, y là các số thực thỏa mãn ( x − 3 ) 2 + ( y − 1 ) 2 = 5 . Giá trị nhỏ nhất của biểu thức P = 3 y 2 + 4 x y + 7 x + 4 y − 1 x + 2 y + 1 là
A. 2 3 .
B. 3 .
C. 114 11 .
D. 3
Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
cho các số thực dương X,y thỏa mãn x<y và\(3x^2\)+\(2y^2\)=5xy.Tính giá trị của biểu thức S=\(\dfrac{y+2x}{y-2x}\)
\(3x^2+2y^2=5xy\)
\(\Leftrightarrow3x^2+2y^2-5xy=0\)
\(\Leftrightarrow2\left(x^2-2xy+y^2\right)+x^2-xy=0\)
\(\Leftrightarrow2\left(x-y\right)^2+x\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[2\left(x-y\right)+x\right]=0\)
\(\Leftrightarrow\left(x-y\right)\left(3x-2y\right)=0\)
\(\Leftrightarrow3x-2y=0\Leftrightarrow x=\dfrac{2y}{3}\) Thay vào S
\(\Rightarrow S=\dfrac{y+\dfrac{4y}{3}}{y-\dfrac{4y}{3}}=-7\)
Đúng 0
Bình luận (0)