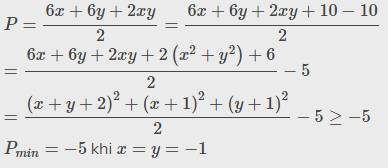Cho x,y thoả mãn 8x^2 +y^2+1/(4x^2)=4. Tìm giá trị nhỏ nhất của A=xy

Những câu hỏi liên quan
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Cho các số thực dương x,y thoả mãn: (x+y-1)^2= xy . Tìm giá trị nhỏ nhất của biểu thức P=1/xy + 1/x^2+y^2 + căn(xy)/x+y
Cho các số thực x và y thoả mãn điều kiện x^2+y^2=2. tìm giá trị nhỏ nhất của biểu thức P=3(x+y)+xy
\(P=\dfrac{6x+6y+2xy}{2}=\dfrac{6x+6y+2xy+10-10}{2}\)
\(=\dfrac{6x+6y+2xy+2\left(x^2+y^2\right)+6}{2}-5\)
\(=\dfrac{\left(x+y+2\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-5\ge-5\)
\(P_{min}=-5\) khi \(x=y=-1\)
Đúng 1
Bình luận (3)
cho các số thực x và y thoả mãn điều kiện x^2+y^2=2. tìm giá trị nhỏ nhất của biểu thức P= 3(x+y)+xy
Cho x,y>0 thoả mãn x+y=4. Tìm giá trị nhỏ nhất của biểu thức: A=xy + 20/xy
cho các số dương x và y thoả mãn \(\frac{1}{x^2}+\frac{1}{y^2}=\frac{1}{2}\) .Tìm giá trị nhỏ nhất của biểu thức A=xy+2017
\(\frac{1}{2}=\frac{1}{x^2}+\frac{1}{y^2}\ge\frac{2}{xy}\)
\(\Leftrightarrow xy\ge4\)
\(\Rightarrow A=xy+2017\ge4+2017=2021\)
Đúng 0
Bình luận (0)
cho x,y thỏa mãn đẳng thức:
8x2+y2+\(\frac{1}{4x^2}\)=4
tìm x,y để tích xy đạt giá trị lớn nhất.
\(4x^2-2+\frac{1}{4x^2}+\left(2x\right)^2+y^2=4\)
\(\left(\left(2x\right)^2-\frac{1}{\left(2x\right)^2}\right)^2+\left(\left(2x\right)-y\right)^2=4-2\left(2x\right)y\)
\(VT\ge0\) đẳng thức khi: 2x=+-1; 2x=y;
\(\Rightarrow4-4xy\ge0\Rightarrow xy\le1\)
DS: x=+-1/2; y+-1
Đúng 0
Bình luận (0)
Cho hai số thực x và y thỏa mãn \(x^2+y^2=1+xy\). Tìm giá trị nhỏ nhất của \(A=x^4+y^4-x^2y^2\)
Cho x,y là các số thực dương thoả mãn x + y = 1. Tìm giá trị nhỏ nhất của biểu thức:
\(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{xy}\)
\(x+y=1\Rightarrow2\sqrt{xy}\le1\Rightarrow\sqrt{xy}\le\frac{1}{2}\)
\(\Rightarrow xy\le\frac{1}{4}\Rightarrow\frac{1}{xy}\ge4\)
Áp dụng bđt cauchy cho 3 số dương:
\(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{xy}\ge3\sqrt[3]{\frac{1}{x^2}.\frac{1}{y^2}.\frac{1}{xy}}=3.\frac{1}{xy}\ge3.4=12\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)